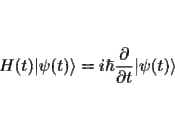Circulation in animals

Diffusion alone is not for transporting chemicals over macroscopic distances in animals – for example, for moving glucose from the digestive tract and oxygen from the lungs to the brain of a mammal.

The time it takes for a substance to diffuse from one place to another is proportional to the square of the distance the chemical will travel – for example, if it takes 1 second for a given quantity of glucose to diffuse 100 micrometers (10-6) it will take 100 seconds for the same quantity to diffuse /mm.

-To solve this problem, macroscopic organisms have a circulatory system, which ensures that no substance must diffuse very far to enter or leave a cell.

- By transporting fluids throughout the body, the circulatory system functionally connects the aqueous environment of the body cells & the organs that exchange gases, absorb nutrients, & dispose of waste.

Circulatory System(http://www.williamsclass.com)Oxygen Molecule ADVENTUREDiaphragm contracts & air is inhaled into the mouth/nose.

A harmonic oscillator in classical mechanics (A-B)...

Hilbert Space

The first few hydrogen atom electron orbitals show...

The oxygen molecule is than pushed through the Larynx into the trachea. Oxygen than passes through the bronchiole tubes in the lungs which than passes through bronchioles which defuse through a thin layer of cells called alveoli. This is where gas exchange occurs.

3. Quantum MechanicsFour basic principles of quantum mechanics are:3.1 Physical StatesEvery physical system is associated with a Hilbert Space, every unit vector in the space corresponds to a possible pure state of the system, and every possible pure state, to some vector in the space.[7] In standard texts on quantum mechanics, the vector is represented by a function known as the wave-function, or ψ-function.

3.2 Physical QuantitiesHermitian operators in the Hilbert space associated with a system represent physical quantities, and their eigenvalues represent the possible results of measurements of those quantities.

3.3 CompositionThe Hilbert space associated with a complex system is the tensor product of those associated with the simple systems (in the standard, non-relativistic, theory: the individual particles) of which it is composed.

3.4 Dynamicsa.Contexts of type 1: Given the state of a system at t and the forces and constraints to which it is subject, there is an equation, ‘Schrödinger's equation’, that gives the state at any other time U|vt> → |vt′>.[8] The important properties of U for our purposes are that it is deterministic, which is to say that it takes the state of a system at one time into a unique state at any other, and it is linear, which is to say that if it takes a state |A> onto the state |A′>, and it takes the state |B> onto the state |B′>, then it takes any state of the form α|A> + β|B> onto the state α|A′> + β|B′>.

b.Contexts of type 2 ("Measurement Contexts"):[9] Carrying out a "measurement" of an observable B on a system in a state |A> has the effect of collapsing the system into a B-eigenstate corresponding to the eigenvalue observed. This is known as the Collapse Postulate. Which particular B-eigenstate it collapses into is a matter of probability, and the probabilities are given by a rule known as Born's Rule:prob(bi) = ||2.

There are two important points to note about these two kinds of contexts:•The distinction between contexts of type 1 and 2 remains to be made out in quantum mechanical terms; nobody has managed to say in a completely satisfactory way, in the terms provided by the theory, which contexts are measurement contexts, and•Even if the distinction is made out, it is an open interpretive question whether there are contexts of type 2; i.e., it is an open interpretive question whether there are any contexts in which systems are governed by a dynamical rule other than Schrödinger's equation.

http://plato.stanford.edu/entries/qm/

English: Hydrogen Density Plots for n up to 4.

English: A GIF animation about the summary of quan...

English: created by Bamse 04:51, 4 August 2006 (UT...