*Aristarchus
*Aristarchus of Samos (310-230 B.C.), was a astronomer often referred to as the Copernicus of antiquity, laid the foundation for much scientific examination of the heavens. According to his contemporary, Archimedes, Aristarchus was the first to propose not only a heliocentric universe, but one larger than any of the geocentric universes proposed by his predecessors.
*Copernicus himself originally gave credit to Aristarchus in his own heliocentric treatise, De revolutionibus caelestibus , where he had written, "Philolaus believed in the mobility of the earth, and some even say that Aristarchus of Samos was of that opinion." Interestingly, this passage was crossed out shortly before publication, maybe because Copernicus decided his treatise would stand on its own merit.
*Plutarch in his De facie in orbe lunae gives reference not only to Aristarchus's theory, but to the way it was received by contemporaries. The general opinion of the time appeared to be that of Dercyllides, who "says that we must suppose the earth, the Hearth of the House of the Gods according to Plato, to remain fixed, and the planets with the whole embracing heaven to move, and rejects with abhorrence the view of those who have brought to rest the things which move and set in motion the things which by their nature and position are unmoved, such a supposition being contrary to the hypotheses of mathematics."
As we can imagine, this did not look good for Aristarchus, and was probably one of the main reasons the heliocentric hypothesis did not re-emerge until the mid 15th century with the Copernican revolution.
*Though some of his reasoning was a bit out of place in his time, Aristarchus nevertheless was able to adapt to the conventions of society and use the methods of known geometry to explain other phenomena. His treatise On the Sizes and Distances of the Sun and Moon, written from a geocentric point of view, was a breakthrough in finding distances to objects in the universe, and his methods were used by later astronomers and mathematicians through the time of Hipparchus and Ptolemy.
*Aristarchus introduced six hypotheses, from which he determined first the relative distances of the sun and the moon, then their relative sizes:
*1) The moon receives its light from the sun.
*2) The earth is positioned as a point in the center of the sphere in which the moon moves.
*3) When the moon appears to us halved, the great circle which divides the dark and bright portions of the moon is in the direction of our eye.
*4) When the moon appears to us halved, its [angular] distance from the sun is then less than a quadrant by one-thirtieth part of a quadrant. (One quadrant = 90 degrees, which means its angular distance is less than 90 by 1/30th of 90, or 3 degrees, and is therefore equal to 87 degrees.) (This assigned value was based on Aristarchus' observations.)
*5) The breadth of the earth's shadow is that of two moons.
*6) The moon subtends one fifteenth part of a sign of the Zodiac. (The 360 degrees of the celestial sphere are divided into twelve signs of the Zodiac each encompassing 30 degrees, so the moon, therefore, has an angular diameter of 2 degrees.)
*Although he proved many propositions (eighteen to be exact), the three most well-known are the following:
*1) The distance of the sun from the earth is greater than eighteen times, but less than twenty times, the distance of the moon from the earth.
*2) The diameter of the sun has the same ratio (greater than eighteen but less than twenty) to the diameter of the moon.
*3) the diameter of the sun has to the diameter of the earth a ratio greater than 19 to 3, but less than 43 to 6.
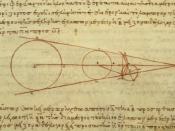
*In his determination of these three factors, Aristarchus developed the Lunar Dichotomy method and the Eclipse Diagram, the latter of which became a much-used method of determining celestial distances up until the seventeenth century.
*Method of Lunar Dichotomy When the moon appears to us in its phase of First Quarter or Last Quarter, it is "dichotomized," or half illuminated. At the moment when the dividing line between light and dark exactly bisects the moon's circle, the angle from Earth to Moon to Sun is exactly 90 degrees. Aristarchus determined that at this precise moment the angular separation between the moon and the sun, that is, the angle from Moon to Earth to Sun, is equal to 87 degrees, as he stated in his fourth hypothesis. Using these angles, he determined (without using trigonometric tables or formulae--they weren't invented yet) that the ratio of the distance ES to EM was greater than 18 to 1, but less than 20 to 1.
*In order to determine the actual values for the sizes of the sun and moon, Aristarchus used two observations: first, that the disk of the moon just covers the sun during a solar eclipse--although this is not always true, for the sun appears larger during an annular eclipse.
*Second, that during a lunar eclipse the shadow of the earth appears to be twice as large as the moon at the moon's distance. With this data he constructed the Eclipse Diagram, which he used to show that the earth is approximately three times larger than the moon, and that the radius of the sun is more than six times larger than the radius of the earth.
*Although his geometry was perfect, Aristarchus' methods of measurement were extremely inaccurate. His basic value for the angle from Sun to Earth to Moon was off by a few degrees (the actual value is 89 degrees, 50 minutes), and the width of the earth's shadow cone at the moon is actually three rather than two moon diameters. Using improved values, we can show that the sun is about 400 times farther from the earth than the moon, and its diameter is approximately 109 times greater than that of earth.
*In terms of heliocentricity or the movement of the earth, the only person to follow Aristarchus' philosophy was Seleucus, who in 150 B.C. attributed the ocean tides to the stirring of air caused by the rotation of the earth and its interaction with the revolution of the moon. Later, in the first century BC, Seneca mentioned the possibility of a rotating earth, but did not necessarily believe that it was possible.
*Overall, Aristarchus was a pioneer both in his depiction of the universe and his geometric approach to the measurement of the heavenly bodies. He contributed a great deal to both geometry and astronomy, and his methods, as adapted by Hipparchus and others, were used well into the 17th century