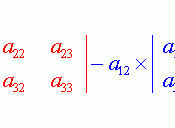An argument given by professor Loren Johnson of the Mathematics Department of the University of California Santa Barbara states: The determinant of the n x n matrix A is the product of it's eigenvalues (Yaquib 303). In order to show if this argument is valid and sound we will need to define some essential terms. I am going to assume that a fair amount of Calculus is know to the reader in order to show whether or not this argument is valid and sound. Matrices are used in linear algebra to discuss systems of equations. The matrix itself is composed of the terms preceding each of the variables in each equation of the system. An example of a system of three equations would be: 2x + 3y + 4z, x +3y and 6x + 2y + 2z. The first row of the matrix for this system is [2 1 6], the second would be [3 3 2] and the third would be [4 0 2] which we will call A.
Solving determinants
Health Professional Shortage
Population with No High School Diploma, Percent by...Using this information we can define the determinant as being the sum of all possible elementary signed products from A. This can only be achieved if A is an n x n matrix, where n represent the number of rows and columns. The signed elementary products of A can be defined as 1 when the permutation of the elementary products is even and -1 when the permutation of the elementary products is odd (Hughes-Hallet 20). These two numbers are then multiplied by their respective permutation and the whole lot is added together. When all calculations are said and done this results in a number for matrix A, in this case -58. This now leads us to the definition of an eigenvalue. Since we have already defined A as a n x...