UNIVERZITET U BEOGRADU
EKONOMSKI FAKULTET
PRISTUPNI RAD IZ PREDMETA OSNOVI STATISTI^KE ANALIZE
TEMA: DESKRIPTIVNA ANALIZA
STUDENTI
Stojiqkovi} Bogdan
Beograd, maj 2005.
�
UVOD
Do spoznaje nekog zakona dolazi se primenom odre|enog nau~nog metoda. Metod ista`ivawa predstavqa na~in tj. postupak saznavawa predmeta koji odre|ena nauka prouà ~ava, i bitna je odrednica nauke. Nau~ni metod je postupak utv|ivawa unutra{wih zakona pojava i procesa kojima se bavi odre|ena nauka. Metodi istra`ivawa u statistici se mogu podeliti na deskriptivnu statistiku i analiti~ku statistiku. Mada se deskriptivna statistika bavi prikupqawem, sre|"""""'''''ivawem i prikazivawem podataka i odre|ivawem parametara skupova, a analiti~ka statistika se bavi obja{wewem varijabiliteta pomo"}u klasifikacionih, korelacionih i drugih pokazateqa i statisti~kim zakqu~ivawem na osnovu uzorka, ne mo`e se napraviti jasna granica izme|u dva metoda. Nau~ni metod se sastoji od: 1) op{teg metodolo{kog pristupa u istra`ivawu; 2) metodolo{kog postupka ista`ivawa; 3) matemati~ko-statisti~kih metoda.
U etapi op{teg metodolo{kog pristupa u istra`ivawu defini{u se ciq, predmet istra`ivawa i jasno se defini{e kojim elementima treba po~eti analizu, koji su to bitni elementiâ¦â¦...
Ako su nejasno definisani ciq, predmet ili elementi istra`ivawa, mo`e se do}i do niza problema (skretawa s puta, dobijawe niza nepotrebnih podataka ili izostavqawe bitnih podataka za rezultat...). "Planom prikupqawa podataka odre|uju se i defini{u modaliteti obele`ja i doga|aji koji }e se obuhvatiti, a u sklopu wihovih definicija i na~in merewa i iskazivawa"1). Merewe se razlikuje od pojave do pojave zavisno od od vrste posmatrane pojave, kao i rezultata koji `elimo da dobijemo (na primer, merewe uspeha u~enika u {koli se razlikuje od merewa stope rasta u privredi). Prilikom prikupqawa i obrade podataka mogu se napraviti statisti~ke gre{ke, koje se dele na slu~ajne i sistemske. Slu~ajne gre{ke nemaju veliki uticaj na ishod istra`ivawa, dok sistematske gre{ke nastaju usled lo{eg sprovo|ewa istra`ivawa, imaju ogroman uticaj na ishod i moraju se otkloniti.
MERNE SKALE
Postoje ~etiri nivoa merewa i prema wima konstruisane ~etiri merne skale gde se kriterijumi rangirawa koriste dogovorno:
Nominalna,
Ordinalna,
Intervalna,
Skala odnosa
NOMINALNA SKALA
Nominalna skala prikazuje samo modalitete neka posmatrane pojave. Zbog toga je ona najnepreciznija. Modaliteti ne prate neki odre|eni redosled, ali se me|usobno iskqu~uju. Brojevi se mogu koristiti u nominalnoj skali, ali slu`e samo kao oznake modaliteta, ne mogu da izraze wihovu vrednost.
PRIMER: klasifikacija `ivotiwa iz porodice ma~aka mo`e svstavati neku `ivotiwu koja pripada toj porodici tj. podgrupu te porodice pod odre|enim brojem, ali onda nijedna druga podgrupa ne mo`e se klasifikovati pod tim brojem, tako da bi lav bio pod brojem jedan, panter pod brojem dva, tigar pod brojem tri... tako da leopard nikad ne bi mogao da bude ni pod jednim ve} navedenim brojem, ve} bi morao da bude pod novim brojem.
ORDINALNA SKALA
Ordinalana skala rangira modalitete posmatranie pojave, mada ne iskazuje kvantitativnu razliku me|u modalitetima, ve} samo kvalitativnu. Ordinalne skale se razlikuju me|usobno i od broja rangova, tj. od veli~ine skale, jer nije isto biti tre}i od deset i tre}i od sto.
PRIMER: na tabeli lige fudbalskih klubova jedne zemqe, (naj~e{}e) prvi na tabeli ide u LIGU [AMPIONA, drugi na tabeli ide u KUP UEFA, ali varira od zemqe do zemqe.
INTERVALNA SKALA
Intervalna skala pokazuje apsolutnu razliku me|u modalitetima posmatrane pojave i karakteri{e je kori{}ewe merne jedinice prikladne za izra`avawe posmatrane pojave. Ipak, nulta vrednost na skali ne zna~i odsustvo pojave, tj. intervalna skala nema pravu nultu vrednost pojave.
PRIMER: merewe vremena nema svoju pravu nultu vrednost, a i razli~ite religije tj. narodi su merili vreme prema wima va`nim doga|ajima, tako da su Stari Grci merili vreme od prve Olimpijade, a Hri{}ani mere vreme od ro|ewa Hristovog.
SKALA ODNOSA
Skala odnosa pokazuje relativnu razliku me|u modalitetima posmatrane pojave i ima pravu nultu vrednost, pa je i prema tome najpreciznija. Merne jedinice koje se koriste su, kao i kod svih ve} pomenutih mernih skala, utv|ene dogovorno.
PRIMER: u Srbiji se, kao i u ostatku kontinentalne Evrope, visina i du`ina izra`avaju u metrima, a te`ina u kilogramima, dok se u Americi visina i du`ina izra`avaju u in~ima i fitima, a te`ina u funtama.
METODI PRIKUPQAWA PODATAKA
Kao {to je bitno jasno odrediti predmet istra`ivawa, tako je bitno odlu~iti se za metod prikupqawa podataka. Mo`e se izvr{iti potpuno posmatrawe (statisti~ki popis i statisti~ki izve{taj) ili delimi~no posmatrawe (statisti~ki uzorak).
STATISTI^KI POPIS
Statisti~ki popis je posmatrawe pojave kroz sve wene elemente u odre|enom trenutku (kriti~ni momenat) i slu`i za pra}ewe relativno stabilnih pojava. Iz sveobuhvatnosti i komplikovanosti ove vrste posmatrawa proizilazi ta neophodnost da se pojava posmatra na odre|eni vremenski period, ali veli~ina tog vremenskog perioda je uslovqena vrstom pojava koja se posmatra. Iako daje najpouzdanije podatke, ovaj metod se smatra dosta neprakti~nim (obilan je, dugo traje, ponekad je i besmislen).
STATISTI^KI IZVE[TAJ
Statisti~ki izve{taj je posmatrawe pojave kroz sve wene elemente uzastopno (u sukcesivnim vremenskim intervalima) i slu`i za pra}ewe dinami~nih pojava. Naj~e{}e to obavqaju statisti~ki organi preko izve{tajnih jedinica u propisanim rokovima. Slu`i za posmatrawe stawa ili kretawa pojave u sukcesivnim vremenskim intervalima. Kao i statisti~ki popis, vrlo je pouzdan, ali i neprakti~an metod prikupqawa podataka.
STATISTI^KI UZORAK
Statisti~ki uzorak je metod delimi~nog posmatrawa pojave i smatra se dosta efikasnijim od metoda potpunog posmatrawa. Elementi statisti~kog uzorka se posmatraju isto kao i elementi statisti~kog popisa, samo {to se pri statisti~kom uzorku posmatraju samo neki elementi pojave (reprezentativni) i na osnovu wih se vr{i statisti~ko zakqu~ivawe o celoj pojavi. Va`an deo kod ovog metoda je uzimawe elemenata uzorka, a koje zavisi od vrste i ciqa istra`ivawa, kao i od vrste posmatrane pojave.
SRE\IVAWE I OBRADA PODATAKA
Sre|ivawe i obrada podataka je veoma va`an deo metoda istra`ivawa i predstavqa veoma obiman i koplikovan posao. Deli se u zavisnosti od mesta sre|ivawa na:
Centralizovano (boqa organizacija, , stru~nost obrade, upotreba jedin-stvenog metoda, efikasnije kori{}ewe tehnike za obradu)
Decentralizovano (br`e objavqivawe podataka)
Kombinovano (jedan deo se vr{i centralizovano, drugi decentra-lizovano)
PRIKAZIVAWE PODATAKA
Statisti~ke serije su rezultat sre'|ivawa podataka. Statisti~ke serije su nizovi statisti~kih podataka koji su sre|eni da "pokazuju strukturu skupa po nekom obele`ju, ili raspored skupa u prostoru, ili promenu skupa u vremenu""2). Serije mo`emo podeliti prema sadr`aju na:
Serije strukture
Vremenske serije
SERIJE STRUKTURE
Serije strukture pokazuju podatke u skupu prema modalitetima, i dele se na atributivne i numeri~ke, a numeri~ke daqe delimo na prekidne i neprekidne. Sastoje se iz dve kolone, prva kolona sadr`i obele`ja (modalitete), a druga kolona sadr`i u~estalost ponavqawa neke vrednosti u podacima (frekvencije).
Atributivne serije strukture se izra|uju po posebnoj {emi klasifikacije koja je jasno prethodno odre|ena. Klasifikacija zavisi od vrste podataka ili ciqa istra`ivawa. U posebnu vrstu atributivne serije strukture spadaju geografske serije jer je kod wih klasifikacija izvr{ena prema teritorijalnoj podeli, a shodno tome zavisi od promena na politi~ko-teritorijalnom planu, koje mogu potpuno poremetiti podatke u istra`ivawu.
PRIMER: vrednost bruto nacionalnog dohotka zemaqa 1997. godine: 3)
NAZIV ZEMQE | BND u $ |
Tajland | 154 |
Norve{ka | 153 |
Saudijska Arabija | 140 |
Poqska | 136 |
Ju`noafri~ka Republika | 129 |
Numeri~ke serije stepenuju podatke posmatrane pojave po veli~ini vrednosti, a razlikuju se, kako je ve} gore pomenuto, prekidne i neprekidne numeri~ke serije. Prekidne serije se stepenuju po vrednostima podatke, od najni`e ka najvi{oj, dok kod neprekidnih serija nastaje problem broja grupa i veli~ine intervala grupa, a koji zajedno treba da zadovoqe i preglednost i da pru`e informacije o posmatranoj pojavi (ovaj problem zna da se pojavi i kod prekidnih serija sa velikim brojem obele`ja). Problem se re{ava odre|ivawem broja grupa po Strxesovom pravilu:
K = 1 + 3,3log N
Gde je N ukupan broj podataka, a potom se razlika najve}eg i najmaweg podatka podeli sa novodobijenim brojem da bi se dobila veli~ina intervala:
i = (Xmax - Xmin)/ K
u praksi se intervali po~iwu sa vredno{}u mawom od najmawe, a zavr{avaju sa vredno{}u ve}om od najve}e, ili se intervali ostavqaju otvoreni. Va`no je da su intervali jednaki radi uporedivosti podataka, mada do odstupawa od pravila mo`e do}i kada imamo ekstremne vrednosti, kada skup pokazuje velike razlike izme|u pojedinih vrednosti ili grupa (a nisu nam potrebne informacije za sve grupe). Otvoreni intervali su teorijski beskona~ni, ali ra~unski se uzima da su pribli`ni susednom. Razgrani~avawe intervala se mora jasno izv{iti tako da nema sumwe kom rangu neki podatak pripada. Ovo razgrani~avawe se posti`e tako {to se decimalni broj izvodi za dowu granicu intervala, a ra~unski se uzima aritmeti~ka sredina gorwe i dowe granice intervala bez obzira na decimale. Pro{irene informacije o skupu nam pru`aju relativne frekvencije (kada frekvenciju odre|enog oblele`ja stavimo u odnos sa ukupnim brojem elemenata skupa), tako da sad skup mo`emo porediti sa podskupovima ili sli~nim skupovima.
PRIMER: srediti podatke za slede}i popis i prikazati kao numeri~ku seriju strukture
20; 13; 9; 6; 6; 8; 2; 7; 9; 15; 18; 16; 17; 7; 8; 11; 6; 13; 18; 16; 5; 7; 19; 7; 9; 11; 10; 7; 6; 8; 6; 14; 11:
Prvo se izra~una broj grupa po Strxesovom pravilu: K = 1 + 3,3log 33 = 6,01 â 6 (jer je N=33)
Potom se izra~una veli~ina intervala: i = (20 - 2)/ 6 = 3 (jer je Xmax= 20, Xmin= 3)
Po{to je dobijeno da formiramo seriju od 6 grupa veli~ine intervala 3:
OBELE@JE | U^ESTALOST (apsolutna frekvencija) | RELATIVNA FREKVENCIJA u % |
2 - 5 | 2 | 6 |
5,1 - 8 | 13 | 39 |
8,1 - 11 | 6 | 19 |
11,1 - 14 | 4 | 12 |
14,1- 17 | 4 | 12 |
17,1 - 20 | 4 | 12 |
ã | 33 | 100 |
VREMENSKE SERIJE
Vremenske serije pokazuju varijacije posmatrane pojave tokom vremena, i dele se na momentne i intervalne. Tako|e se sastoje iz dve kolone, prva kolona sadr`i odrednice vremena, a druga kolona sadr`i veli~inu pojave u posmatranom periodu.
Momentne serije prikazuju promene veli~ina u ta~no odre|enim izastopnim momentima vremena. Rezultat su vi{e uzastopnih popisa, i wihovo sumirawe je besmisleno jer ne pru`aju nikakvu validnu informaciju za istra`ivawe u kojem se upotrebqavaju.
PRIMER: na kraju svake smene u ugostiteqskim objektima (tipa gril restorana, pekara, poslasti~arnica...) vr{i se popis preostale, neprodate, robe. Ako uzmemo da radni dan ima samo jednu smenu, dobijamo:
DAN | PREOSTALA KOLI^INA ARTIKLA A |
20. 02. 2002. | 150 |
21. 02. 2002. | 136 |
22. 02. 2002. | 149 |
23. 02. 2002. | 115 |
Intervalne serije pokazuju tok kretawa pojave u uzastopnim intervalima. Rezultat su neke vrste statisti~kog izve{taja, i wihovo sumirawe ima smisla u ciqu pru`awu informacija.
PRIMER: proizvodwa bakra u Jugoslaviji 1979-1989. godine u hiqadama tona:4)
GODINA | PROIZVODWA BAKRA |
1979. | 16.446 |
1980. | 19.559 |
1981. | 18.337 |
1982. | 19.733 |
1983. | 23.443 |
1984. | 25.279 |
1985. | 26.166 |
1986. | 27.158 |
1987. | 28.253 |
1988. | 29.523 |
1989. | 30.052 |
TABELARNO PRIKAZIVAWE
Tabelarno prikazivawe je jedan od na~ina prikazivawa serija u koncentrisanom vidu radi lak{eg rada sa sakupqenim podacima u vidu jasnosti podataka i lak{eg upore|ivawa podataka. Svaka tabela se sastoji od: poqa tabele, nastalih ukr{tawem redova i kolona tabele; naslova tabele, koji nam govori {ta posmatramo ili tuma~imo, a koji se mo`e nalaziti iznad ili ispod tabele; prvog reda (zaglavqa) i prve kolone (pretkolone) u koje unosimo obele`ja; i (ako je mogu}e usled vrste podataka) posledweg reda (ili kolone), koji sadr`i sumirane vrednosti poqa tabele. Statisti~ke tabele se prema nameni dele na obradne (obimne, sa detaqnim podacima, slu`e za sastavqawe analiti~kih tabela) i analiti~ke (sa`etije, ciq im je da istaknu vezu izme|u obele`ja i pospe{uju wihovu analizu). Statisti~ke tabele se prema sadr`aju dele na proste, slo`ene i kombinovane.
Proste tabele sadr`e podatke jedne serije koji se odnose na seriju strukture ili vremensku seriju.
PRIMER: u~inak dva prodavca u maloj firmi:
PRODAVAC | OBIM PRODAJE |
Prodavac 1 | 1306 |
Prodavac 2 | 2560 |
UKUPNO | 3866 |
Slo`ene tabele nastaju spajawem dve ili vi{e prostih tabela, koje pokazuju rali~ite podatke, ali su ras~lawene prema istom obele`ju i u sadr`inskoj su vezi.
PRIMER: obim prodaje dva artikla u tri grada Srbije:
ARTIKL | BEOGRAD | NOVI SAD | SMEDEREVO | UKUPNO |
Artikl 1 | 30 | 26 | 13 | 69 |
Artikl 2 | 64 | 70 | 50 | 184 |
UKUPNO | 94 | 96 | 63 | 253 |
Kombinovane tabele sadr`e podatke dobijene ukr{tawem dva ili vi{e obele`ja ozna~enim i u zaglavqu i u pretkoloni tabele. Imaju ogroman analiti~ki zna~aj ako se ne zakomplikuju previ{e ~ime postaju nepregledne.
PRIMER: struktura studenata na tri Beogradska univerziteta iz ~etiri sredwe {kole:
Fakultet Sredwa {kola | ||||
EKONOMSKI | FILOLO[KI | PRAVNI | UKUPNO | |
Ekonomska | 638 | 24 | 97 | 759 |
Tehni~ka | 24 | 16 | 134 | 174 |
Filolo{ka | 13 | 967 | 59 | 1039 |
Gimnazija | 409 | 382 | 561 | 1352 |
UKUPNO | 1084 | 1389 | 851 | 3324 |
GRAFI^KO PRIKAZIVAWE
Grafi~ko prikazivawe je jo{ jedan na~in prikazivawa serija u vidu geometrijskih oblika, oznaka na geografskim kartama ili slika tj. simboli~nih figura. Geografske serije se prikazuju na kartogramima, grafi~kim prikazima pomo}u oznaka na geografskim kartama. Prikazivawe serija u vidu geometrijskih oblika je dosta rasprostraweniji na~in koji pru`a vi{e mogu}nosti za upore|ivawe. Ti geometrijski oblici se nazivaju dijagramima, a izbor vrste dijagrama zavisi od vrste i ciqa istra`ivawa i podataka. Dijagrami mogu biti:
linijski (imaju jednu dimenziju i slu`e za prikazivawe modalitete jednog obele`ja)
povr{inski ili histogrami (mogu prikazivati vi{e obele`ja deqewem na mawe osen~ene povr{ine)
prostorni ili stereogrami (mogu prikazivati trodimenzionalno podatke)
u vidu ta~aka ili stigmogrami
Grafi~ko prikazivawe se mo`e vr{iti u koordinatnom i izvan koordinatnog sistema. Grafi~ki prikazi u pravouglom ili polarnom koordinatnom sistemu slu`e za prikaz i analizu statisti~kih podataka raspore|enih po frekvencijama ili u vremenskim serijama i dosta su precizniji od grafi~kih prikaza izvan koordinatnog sistema koji naj~e{}e nalaze primenu na geografskim kartama primenom kartograma.
GRAFI^KO PRIKAZIVAWE U PRAVOUGLOM KOORDINATNOM SISTEMU
Ovi prikazi se vr{e unutar pravog kvadranta pravouglog koordinatnog sisitema, gde se na apscisnoj osi nalaze obele`ja (modaliteti), a na ordinatnoj osi se nalaze u~estalost ponavqawa neke vrednosti u podacima (frekvencije). Neka gruba podela se mo`e izv{iti unutar grafi~kih prikaza u pravouglom koordinatnom sistemu na grafi~ko prikazivawe:
Numeri~kih serija sa prekidnim obele`jem
Numeri~kih serija sa neprekidnim obele`jem
Vremenskih serija
GRAFI^KO PRIKAZIVAWE NUMERI^KIH SERIJA SA PREKIDNIM OBELE@JEM
Prikazivawe se vr{i pomo}u:
Stigmograma (ozna~avawem ta~aka za vrednosti obele`ja podataka posmatrane pojave, naj~e{}e sre|enih u tabelama)
Ordinatama (sli~no stigmogramima, gde su ta~ke stigmograma ordinatama povezane sa apscisnom osom)
Dotplotom (ta~ke se uzdi`u sa apscisne ose do vrednosti podataka, prikaz u kom nema ordinatne ose, neprakti~an kod velikih vrednosti)
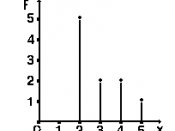
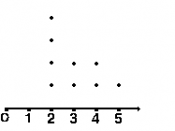
PRIMER: za slede}e podatke iz tabele veli~ine porodica u selima na jugu Srbije (na osnovu uzorka od 10 porodica) napraviti grafi~ke prikaze u pravouglom koordinatnom sistemu (pomo}u: 1) stigmograma; 2) ordinata; 3) dotplota)
BROJ ^LANOVA PORODICE (H) | BROJ PORODICA (F) |
2 | 5 |
3 | 2 |
4 | 2 |
5 | 1 |
GRAFI^KO PRIKAZIVAWE NUMERI^KIH SERIJA SA NEPREKIDNIM OBELE@JEM
Prikazivawe se vr{i pomo}u:
Histograma (pravougaonici ~ija je osnova veli~ina grupnog intervala, a visina frekvencija istog intervala; povr{ina jednog pravougaonika je proporcionalana frekvenciji tog grupnog intervala, a povr{ina svih pravougaonika jednaka je ukupnoj frekvenciji posmatrane populacije)
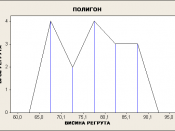
Poligona (mnogougaona povr{ina ograni~ena izlomqenom linijom koja povezuje sredine grupnih intervala u vrednosti frekvencije i apscisnom osom; ukupna povr{ina poligona jednaka je ukupnoj povr{ini histograma za istu posmatranu pojavu tj. jednaka je ukupnoj frekvenciji posmatrane populacije; ako je u pitawu otvoreni interval, sredine grupnog intervala se ne spajaju sa apscisnom osom, nego vise u vazduhu, a ako je zatvoren interval, onda se krajevi izlomqene linije spajaju sa susednim sredinama intervala na apscisnoj osi)
Teorijskom krivom (sli~no poligonu, izlomqena linija se unosi kao kontinuirana kriva; pri kori{}ewu teorijske krive polazi se od pretpostavke da su grupni intervali beskrajno mali, a da je wihov broj beskrajno veliki; teorijska kriva ukazuje na oblik rasporeda frekvencija, {to je veoma va`no u statistici)
Kumulante (koristi kumulirane frekvencije od najni`e navi{e (kumulirawe ispod) ili od najvi{e nani`e (kumulirawe iznad) sukcesivnim sabirawem gde kona~na suma kumulirawa mora biti jednaka ukupnom zbiru frekvencija; u preseku kumulante ispod i iznad dobija se medijana populacije)
PRIMER: za slede}u grupu od 16 regruta date su wihove te`ine : 65; 78; 90; 67; 83; 80; 72; 75; 69; 81; 80; 85; 90; 87; 77; 69. srediti i grupisati podatke i napraviti grafi~ke prikaze u pravouglom koordinatnom sistemu (pomo}u: 1) histograma; 2) poligona; 3) teorijske krive; 4) kumulante ispod i iznad):
Prvo se izra~una broj grupa po Strxesovom pravilu: K = 1 + 3,3log 16 = 4,97 â 5 (jer je N=16)
Potom se izra~una veli~ina intervala: i = (90 - 65)/ 5 = 5 (jer je Xmax= 90, Xmin= 65)
Po{to je dobijeno da formiramo seriju od 5 grupa veli~ine intervala 5, a za potrebe kumulante formira}emo u tabeli dve nove kolone, za kumulantu iznad i za kumulantu ispod:
VISINA REGRUTA | BROJ REGRUTA | KUMULANTA ISPOD | KUMULANTA IZNAD |
65 - 70 | 4 | 4 | 16 |
70.1 - 75 | 2 | 6 | 12 |
75.1 - 80 | 4 | 10 | 10 |
80.1 - 85 | 3 | 13 | 6 |
85.1 - 90 | 3 | 16 | 3 |
ã | 16 |
1)
2)
3)
4)
GRAFI^KO PRIKAZIVAWE VREMENSKIH SERIJA
Prikazivawe se vr{i pomo}u:
Aritmeti~kih linijskih dijagrama (linijski dijagram sa aritmeti~kom skalom na ordinatnoj osi, gde se na apscisnoj osi nalaze oznake za vreme, a na ordinatnoj osi apsolutne vrednosti veli~ine posmatrane pojave u pojedinim momentima ili uzastopnim intervalima; ako ordinatna osa sadr`i velike vrednosti, a rasponi moraju biti jednaki, po~etak prekidamo sa dve crte da bi izbacili neposmatrane vrednosti i time dobili ve}u preglednost dijagrama; po{to pokazuje apsolutne vrednosti, ovaj dijagram pokazuje za koliko, a ne koliko puta je ve}a ili mawa posmatrana pojava u momentu)
Polulogaritamskih linijskih dijagrama (sli~an aritmeti~kom linijskom dijagramu, sem {to umesto apsolutnih vrednosti, na ordinatnoj osi se nalazi logaritamska skala, pa se preko ovog dijagrama mogu pratiti proporcionalne promene posmatrane pojave, ~ak i vi{e vremenskih serija kod kojih postoje apsolutne razlike u nivoima na kojima se kre}u podaci ili ako su kori{}ene razli~ite merne jedinice; ordinatna osa ne mo`e po~eti od nule)
PRIMER: grafi~ki predstaviti promenu prodaje posmatrane firme A (tabela 1) po mesecima 2005. godine, a potom uporediti sa promenom prodaje firme B (tabela 2):
TABELA 1 | TABELA 2 | |||||
PERIOD | PRODAJA (X1) | log X1 | PERIOD | PRODAJA (X2) | log X2 | |
Januar | 130 | 2.11 | Januar | 305 | 2.48 | |
Februar | 168 | 2.22 | Februar | 334 | 2.52 | |
Mart | 170 | 2.23 | Mart | 370 | 2.57 | |
April | 199 | 2.29 | April | 380 | 2.58 | |
UKUPNO | 667 | UKUPNO | 1389 |
GRAFI^KO PRIKAZIVAWE U POLARNOM KOORDINATNOM SISTEMU
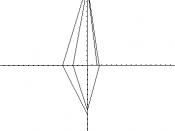
Kod vremenskih serija kod kojih je izra`en sezonski karakter promena koristi se polarni dijagram. Zavisno od du`ine vremenskog perioda koji se posmatra, krug dijagrama se podeli na potreban broj jednakih delova (za kvartale ~etiri, za mesece dvanaest...) koji se nazivaju potege. Po potegama unosimo merne jedinice skale, a na ostale unosimo ta~ke koje ozna~avaju vrednosti pojave, spajawem ta~aka dobijamo izlomqenu krivu kojapokazuje razvoj promene. Radi lak{eg rada sa dijagramom, mo`e se ucrtati krug na dijagramu koji bi ozna~avao prose~nu vrednost pojave, pa bi se prema tome moglo videti koji delovi su bili iznad (izvan kruga), a koji ispod proseka (unutar kruga).
PRIMER: posmatrati promenu u poslovawu fotografskih radwi po godi{wim dobima:
GODI[WE DOBA | POSLOVAWE |
PROLE]E 2002. | 40 |
LETO 2002. | 300 |
JESEN 2002. | 80 |
ZIMA 2002. | 180 |
PROLE]E 2003. | 50 |
LETO 2003. | 310 |
JESEN 2003. | 120 |
ZIMA 2003. | 200 |
GRAFI^KO PRIKAZIVAWE VAN KOORDINATNOG SISTEMA
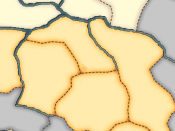
Kod geografskih serija se za grafi~ko prikazivawe koriste kartogrami. Osnovu ~ini geografska karta sa podru~ijima ~ije su granice jasno utvr|ene. Koja vrste su podru~ja zavisi od ciqa istra`ivawa. Podaci o veli~ini pojave se unose u podru~ja {rafurama, ta~kama ili obi~nim dijagramom (simboli raznih vrsta). Ako se ozna~ava sen~ewem ili bojewem, intezitet ozna~avawa treba da bude pribli~an intezitetu posmatrane pojave. Kartogrami se mogu upore|ivati radi posmatrawa razvoja posmatrane promene u vremenskim intervalima koji pak se uzimaju shodno vrsti podataka ili ciqu istra`ivawa (promena nadmorske visine se posmatra na du`e vremenske periode, populacija na otprilike deceniju, a koli~ina padavina na kvartale...). Popularan na~in je prikazivawe slikama (intezitet se ozna~ava razli~itim veli~inama slike ili rali~itim brojem istih slika) pojave koja se posmatra, ali ovaj na~in je najneprecizniji.
PRIMER: dat je kartogram prose~ne visinske strukture regiona sa podelom na 0-500m; 500-1500m; preko 1500m: 5)
DESKRIPTIVNE MERE
U istra`ivawu nam je ciq da dobijemo jedinstvenu sliku o prikupqenim odacima jer gomila podataka, bez obzira kako sre|ena i grafi~ki i tabelarno predstavqena, ote`ava zakqu~ivawe o posmatranoj pojavi. U tu svrhu ras~lawujemo i upore|ujemo podatke i tar`imo pravilnosti i zakonitosti pojave. ^itave serije podataka nastojimo da zamenimo mawim brojem numeri~kih karakteristika koje bi predstavqale seriju {to je mogu}e boqe. Za koju vrstu tih reprezentativnih karakteristika }emo se opredeliti zavisi prvenstveno od ciqa istra`ivawa, ali i od same prirode podataka koje smo prikupili. "Pokazateqe rasporeda frekvencija koji pokazuju ceo osnovni skup nazivamo parametrima skupa i svstavamo ih u tri grupe"6):
Mere centralne tendencije rasporeda
Mere disperzije
Mere oblika rasporeda
Deskriptivne mere koje se odnose na sve jedinice skupa nazivamo parametri skupa, a koje se odnose uzorak statistike uzorka.
MERE CENTRALNE TENDENCIJE
Mere centralne tendencije rasporeda nazivamo druga~ije i sredwim vrednostima. One posmatraju osobine podataka da se grupi{u oko vrednosti koja najboqe predstavqa sve podatke. Takva vrednost nam omogu}ava da upore|ujemo seriju sa drugom serijom (naravno, opet preko vrednosti koja najboqe predstavqa tu drugu seriju), pokazuje lokaciju skupa. Prema na~inu na koji dolazimo do wih, sredwe vrednosti se dele na izra~unate i pozicione. U izra~unate sredwe vrednosti spadaju: aritmeti~ka sredina, geometrijska sredina i harmonijska sredina. U pozicione sredwe vrednosti spadaju: modus i medijana. Svaka sredwa vrednost posebno ima svoje karakteristi~ne osobine (dobre i lo{e) koje se moraju uzeti u obzir pri opredeqivawu u istra`ivawu, ali sve moraju da imaju slede}e osobine: da su dobijene objektivnim matemati~kim putem, da se dobijena sredwa vrednost serije nalazi u intervalu od najmawe do najve}e vrednosti te serije, i da ako su podaci u seriji svi jednaki, onda je i sredwa vrednost ista kao i vrednost obele`ja.
ARITMETI^KA SREDINA
Aritmeti~ka sredina (ili prosek) je naj{ire upotrebqena mera centralne tendencije u istra`ivawu, ali i u svakodnevnom `ivotu. Dobija se kada se zbir svih posmatranih podataka podeli sa brojem posmatranih podataka. Podaci mogu biti grupisani i negrupisani, a aritmeti~ke srednie se mogu izra~unavati za ceo skup ili uzorak (zavisno {ta posmatramo) preko slede}ih formula:
Aritmeti~ka sredina skupa za negrupisane podatke ü = ã x / N | Aritmeti~ka sredina skupa za grupisane podatke ü = ã fi xi / N | Aritmeti~ka sredina uzorka za negrupisane podatke | Aritmeti~ka sredina uzorka za grupisane podatke = ã fi xi / n |
Gde je N broj podataka u skupu, n broj podataka u uzorku, fi frekvencija i-tog podatka. Kao oznaka za aritmeti~ku sredinu skupa koristi se gr~ko slovo ü (koje se ~ita mi), a za aritmeti~ku sredinu uzorka koristi se
suma odstupawa podataka od proseka uvek je jednaka nuli
za grupisane ã fi (xi - ü) = 0; za negrupisane ã (xi - ü) = 0
suma kvadrata odstupawa podataka od proseka mawa je od sume kvadrate odstupawa podataka od bilo koje vrednosti u seriji ili bilo koje druge sredwe vrednosti (pod uslovom da je ta vrednost razli~ita od proseka)
ã (xi - ü)2 < ã (xi - x0)2 (gde je x0 ta vrednost razli~ita od proseka)
Ako su dva obele`ja ili dve serije (h i u) povezane linearnom funkcijom, onda su i wihove aritmeti~ka sredine povezane istom funkcijom
za y=a+bx va`i üy=a+büx (üy prosek od y; üx prosek od x)
GEOMETRIJSKA SREDINA
Geometrijska sredina izravnava relativne i proporcionalne promene izme|u vrednosti podataka posmatrane serije. Dobija se kao pozitivna vrednost korena proizvoda svih vrednosti obele`ja ~iji je izlo`iteq broj podataka ili antilogaritmovawem po slede}oj formuli:
Geometrijska sredina skupa za negrupisane podatke | Geometrijska sredina skupa za negrupisane podatke (antilogaritmovawem) | Geometrijska sredina skupa za grupisane podatke | Geometrijska sredina skupa za grupisane podatke (antilogaritmovawem) |
Gde je N broj podataka, x1 * x2 * ... * xn je proizvod vrednosti obele`ja X, fi frekvencija i-tog podatka. Najve}i nedostatak geometrijske sredine je {to (po{to se izra~unava kao proizvod) nijedna vrednost obele`ja ne sme biti jednaka nuli ili negativna vrednost. geometrijska sredina ima (pored ve} navedenih osobina koje imaju sve sredwe vrednosti) jo{ tri osobine:
Mawa je ili jednaka aritmeti~koj sredini
Proizvod odnosa geometrijske sredine prema mawim vrednostima obele`ja jednak je odnosu ve}ih vrednosti obele`ja prema geometrijskoj sredini
Zbog svojih osobina, geometrijska sredina se slabo koristi kao pokazateq rasporeda frekvencija, ali se naj~e{}e koristi za izravnavawe indeksnih brojeva i za izra~unavawe stope rasta na osnovu lan~anih indeksa, preko formule:
rg = G - 100
Gde je G geometrijska sredina izra~unata za vrednosti lan~anih indeksa ili:
Gde je N broj podataka, Y1 prva vrednost u vremenskoj seriji, a YN posledwa vrednost u vremenskoj seriji. Geometrijska stopa rasta je relativna veli~ina koja se koristi za procenu broja posmatrane pojave izme|u dva popisa ako se rast kre}e pribli`no po geometrijskoj progresiji (naj~e{}e je u pitawu broj stanovnika).
HARMONIJSKA SREDINA
Harmonijska sredina je recipro~na vrednost aritmeti~ke sredine recipro~nih vrednosti obele`ja. Izra~unava se:
Harmonijska sredina za negrupisane podatke | Harmonijska sredina za grupisane podatke |
Gde je N broj podataka, a fi frekvencija i-tog podatka. Harmonijska sredina nema {iroku primenu u istra`ivawu, ali se koristi za izra~unavawe indeksnih brojeva i kod recipro~nih pokazateqa obele`ja. Besmisleno je ra~unati harmonijsku sredinu za vrednosti obele`ja nula.
MODUS
Modus je poziciona sredwa vrednost koja se kao pokazateq lokacije javqa na osnovu odre|ivawa pozicije koju zauzima u seriji. Modus (na osnovu zna~ewa moda) je vrednost obele`ja koja je najtipi~nija u posmatranoj seriji jer ima najve}u u~estalost. Zavisno od toga koliko vrednosti obele`ja ima najve}u u~estalost, serije mogu biti unimodalne (samo jedna vrednost obele`ja sa najve}om u~estalo{}u), bimodalne (dve vrednosti obele`ja) i multimodalne (vi{e vrednosti obele`ja imaju najve}u u~estalost). Serije sa vrednostima obele`ja koja imaju jednaku u~estalost u seriji ka`emo da nema modus. Odre|ivawe za serije negrupisanih podataka je po principu uzimawa vrednosti obele`ja sa najve}om u~estalo{}u za modus. Za serije grupisanih podataka modus se tra`i preko grupnog intervala sa najve}om u~estalo{}u koji se naziva modalnim intervalom po formuli:
Modus Mo= L1 + (f2 - f3) / [(f2 - f1) + (f2 - f3)]i |
Gde je L1 dowa granica modalnog intervala, f1 u~estalost predmodalnog intervala, f2 u~estalost modalnog intervala, f3 u~estalost poslemodalnog intervala, a i je du`ina grupnog intervala. Modus se grafi~ki mo`e najlak{e odrediti preko histograma u preseku linije po~etne vrednosti modalnog intervala i po~etne vrednosti poslemodalnog intervala sa linijom krajwe vrednosti modalnog intervala i krajwe vrednosti predmodalnog intervala. Dobijena ta~ka na apscisi pokazuje modus serije. Najve}i nedostaci modusa su to {to u nekim serijama je nemogu}e odrediti modus i {to je veoma va`no kako grupi{emo podatke, jer ista serija grupisana na dva razli~ita na~ina pokazuje razli~ite moduse, a najve}e prednosti su {to na modus ne uti~u ekstremne vrednosti i {to se mo`e odre|ivati na svim skalama, pa ~ak i nominalnoj. Uzavisno od ciqa istra`ivawa, modus se mo`e pokazati kao najboqa mogu}a sredwa vrednost.
MEDIJANA
Medijana je druga poziciona sredwa vrednost. Medijana je ona vrednost obele`ja koja se nalazi ta~no u sredini sre|ene serije po veli~ini, tj. deli seriju na polovinu koja ima ve}u vrednost od medijane i polovinu koja ima mawu vrednost od medijane. Kod serija sa~iwenih od neparnog broja podataka, medijana je sredi{wa vrednost (npr. u seriji od 7 podataka, 4. podatak je mesto medijane, pa je vrednost 4. podatka medijana...), ali kod serija sa~iwenih od parnog broja podataka, medijana je aritmeti~ka sredina dve sredi{we vrednosti (npr. u seriji od 8 podataka, aritmeti~ka sredina vrednosti 4. i 5. podatka je medijana...). Kada imamo sre|ene serije sa velikim brojem podataka, mo`emo ra~unskim putem da na|emo gde je medijana kumulirawem kolone od najni`e frekvencije navi{e (kumulirawe ispod) tako {to tra`imo gde se obuhvata polovina ukupne frekvencije, tj. koje obele`je obuhvata polovinu ukupne frekvencije. Za serije grupisanih podataka, medijana se odre|uje po formuli:
Medijana Me = L1 + [(N/2 - ãf1) / fMe] i |
Gde je L1 dowa granica medijalnog intervala, N broj ~lanova serije, ãf1 zbir frekvencija predmedijalnog intervala, fMe frekvencija medijalnog intervala, a i je du`ina grupnog intervala. Medijana se grafi~ki najlak{e odrediti preko kumulante, u preseku kumulante iznad i kumulante ispod dobija se ta~ka koja na apscisi pokazuje medijanu. Najve}i nedostatak medijane je {to se ne mo`e odrediti za otvorene intervale koji sadr`e vi{e od polovine podataka, a najve}a prednost je {to na medijanu ne uti~u ekstremne vrednosti.
MERE DISPERZIJE
Mere disperzije nazivamo druga~ije i merama raspr{enosti. Wima merimo varijacije posmatranih serija, jer dve serije mogu imati iste sredwe vrednosti, ali razli~itu disperziju serije. Prema tome kako iskazuju tu disperziju, delimo ih na apsolutne mere disperzije i relativne mere disperzije. Apsolutne mere disperzije pokazuju apsolutne iznose u mernim jedinicama posmatranih obele`ja. One se dele na izra~unate i pozicione. Pozicione apsolutne mere disperziju su interval varijacije i interkvartilna razlika, a izra~unate apsolutne mere disperzije su sredwe apsolutno odstupawe, varijansa i standardna devijacija. Relativne mere disperzije su koeficijent varijacije, koeficijent interkvartilne varijacije i standardizovano odstupawe.
INTERVAL VARIJACIJE
Interval varijacije pokazuje raspon podataka od najmaweg do najve}eg u seriji. Dobija se kao razlika najmawe i najve}e vrednosti obele`ja u seriji:
Interval varijacije i = xmax - xmin |
Interval varijacije daje grubu sliku o disperziji serije. Najve}i nedostaci su {to se mo`e izra~unavati samo za kona~ne razmake i {to na wu uti~u ekstremne vrednosti.
INTERKVARTILNA RAZLIKA
Interkvartilna razlika se izra~unava kao razlika tre}eg i prvog kvartila serije. Kvartili su serija podeqena na ~etiri jednaka dela. Medijana serije se naziva drugim kvartilom. Analogno tome, prvi kvartil deli seriju sre|enu po veli~ini na ~etvrtinu koja ima mawu vrednost od prvog kvartila i tri ~etvrtine koje imaju ve}u vrednost od prvog kvertila; tre}i kvartil deli seriju sre|enu po veli~ini na ~etvrtinu koja ima ve}u vrednost od tre}eg kvartila i tri ~etvrtine koje imaju mawu vrednost od tre}eg kvartila. Preko formula:
Prvi kvartil Q1 = L1 + [(N/4 - ãf1) / fQ1] i | Drugi kvartil (medijana) Me = L1 + [(N/2 - ãf1) / fQ2] i | Tre}i kvartil Q3 = L1 + [(3N/4 - ãf1) / fQ3] i |
Gde je L1 dowa granica kvartilnog intervala, N broj ~lanova serije, ãf1 zbir frekvencija predkvartilnog intervala, fQ frekvencija kvartilnog intervala, a i je du`ina grupnog intervala. Preko svega toga, interkvartilna razlika se dobija:
Interkvartilna razlika iq = Q3 - Q1 |
Po{to kvartili imaju iste osobine kao i medijana, ni na interkvartilnu razliku ne uti~u ekstremne vrednosti.
SREDWE APSOLUTNO ODSTUPAWE
Sredwe apsolutno odstupawe je izra~unata apsolutna mera disperzije koja pokazuje disperziju prema odstupawu od aritmeti~ke sredine, pa je zbog toga (kao i sve izra~unate apsolutne mere disperzije) boqa od pozicionih apsolutnih mera disperzije. Izra~unava se po formuli:
Sredwe apsolunto odstupawe za negrupisane podatke | Sredwe apsolunto odstupawe za grupisane podatke |
Gde je N broj ~lanova serije, fi frekvencija i-tog podatka, a ü aritmeti~ka sredina. Pri izra~unavawu odstupawa podataka od aritmeti~ke sredine koristi se apsolutna vrednost, jer je (kao {to je ve} pomenuto kod osobina aritmeti~ke sredine) zbir odstupawa jednak nuli, a da bi se izbeglo to, za sredwe apsolutno odstupawe se koristi zbir apsolutnih vrednosti odstupawa podataka od aritmeti~ke sredine.
VARIJANSA
Varijansa pokazuje disperziju prema odstupawu od aritmeti~ke sredine, ali (za razliku od sredweg apsolutnog odstupawa gde se koristi zbir apsolutnih vrednosti odstupawa podataka od aritmeti~ke sredine) kod varijanse se koristi zbir kvadrata vrednosti odstupawa podataka od aritmeti~ke sredine. Dobija se po formuli:
Varijansa skupa za negrupisane podatke ÃÂ2 =1/ N ã (xi - ü)2 | Varijansa skupa za grupisane podatke ÃÂ2 =1/ N ãfi (xi - ü)2] | Varijansa uzorka za negrupisane podatke s2 =1/ (n-1) ã (xi - | Varijansa uzorka za grupisane podatke s2 =1/ (n-1) ãfi (xi - |
Gde je N broj podataka u skupu, n broj podataka u uzorku, fi frekvencija i-tog podatka, ü aritmeti~ka sredina skupa, a
STANDARDNA DEVIJACIJA
Standarna devijacija je pozitivan koren varijanse i time je otklowen najve}i nedostatak varijanse (merne jedinice na kvadrat). Oznaka za standardnu devijaciju sjupa je ÃÂ, a za standardnu devijaciju uzorka je s. Iako je standardna devijacija naj~e{}e kori{}ena apsolutna mera disperzije, ona nam sama ne mo`e re}i da li je dobijena vrednost disperzije velika ili ne (jer standardna devijacija zavisi od veli~ine vrednosti obel`ja serije), ve} se u tu svrhu koriste relativne mere disperzije.
KOEFICIJENT VARIJACIJE
Koeficijent varijacije je odnos standardne devijacije i aritmeti~ke sredine. Dobija se po formuli:
Koeficijent varijacije V = à/ ü |
Gde je àstandardna devijacija, a ü aritmeti~ka sredina. Koeficijent varijacije slu`i za upore|ivawe disperzija dve ili vi}e serija, a wegova najve}a prednost (budu}i da je re~ o relativnoj veli~ini, tj. veli~ini izra`enoj u procentima) je {to se mogu upore|ivati serije ~ije merne jedinice nisu iste.
KOEFICIJENT INTERKVARTILNE VARIJACIJE
Koeficijent interkvartilne varijacije je druga mera kojom se porede serije:
Koeficijent interkvartilne varijacije VQ = (Q3 - Q1) / (Q3 + Q1) |
STANDARDIZOVANO ODSTUPAWE
Standardizovano odstupawe se druga~ije naziva i normalizovano odstupawe. Slu`i da se oceni varijacija sa stanovi{ta zasebnih podataka. Dobija se po formuli:
Standardizovano odstupawe Z = (X - ü) / à|
Gde je àstandardna devijacija, a ü aritmeti~ka sredina. Za sve relativne mere va`i pravilo da se kre}u u intervalu od 0 do 1, ili od 0% do 100%. [to je dobijena vrednost bli`a 0, disperzija je mala, {to je daqa od 0 sve je ve}a. Ako su svi podaci u seriji jednaki, dobijena vrednost }e iznositi 0, tj. nema disperzije u seriji.
MERE OBLIKA RASPOREDA
Mere oblika rasporeda obuhvataju mere asimetrije rasporeda i mere spqo{tenosti rasporeda. Obe mere su relativne.
MERE ASIMETRIJE RASPOREDA
Mere asimetrije rasporeda su relativne mere kojima se ispituje simetri~nost oblika rasporeda. Simetri~an raspored ima frekvencije vrednosti obele`ja ravnomerno raspore|ene od aritmeti~ke sredine sa obe strane (kod simetri~nih rasporeda aritmeti~ka sredina, modus i medijana su jednake). Kod asimetri~nih rasporeda frekvencije vrednosti obele`ja grupi{u se iznad ili ispod aritmeti~ke sredine. Ka`emo da je raspored asimetri~an u desno kada je aritmeti~ka sredina ve}a od modusa, ili druga~ije raspored je pozitivno asimetri~an. Ka`emo da je raspored asimetri~an u levo kada je aritmeti~ka sredina mawa od modusa, ili druga~ije raspored je negativno asimetri~an. Za odre|ivawe mera oblika rasporeda koriste se odstupawa vrednosti obele`ja od aritmeti~ke sredine na odre|eni stepen ili centalni momenti rasporeda. Formula za dobijawe centralnih momenata rasporeda:
Centralni momenti rasporeda Mn =1/ N ã (xi - ü)n |
Gde je N broj podataka u skupu, n broj momenta koji posmatramo, ü aritmeti~ka sredina skupa. Za nulti momenat, vrednost je uvek jedan. Za prvi momenat, vrednost je uvek nula. Za drugi momenat, vrednost je uvek jednaka vrednosti varijanse skupa. Mera asimetrije rasporeda se dobija po formuli:
Mera asimetrije rasporeda ñ3 = M3 / ÃÂ3 |
Gde je M3 tre}i centralni momenat rasporeda, ÃÂ3 je standardna devijacija na tre}i stepen. Kao oznaka za meru asimetrije rasporeda koristi se gr~ko slovo ñ3 (koje se ~ita alfa tri). Tre}i stepeni se poni{tavaju i dobijamo relativnu meru. Kada se ñ3 kre}e u intervalu od -- 0.5 do 0.5, ka`emo da je raspored umereno asimetri~an, za sve van tog intervala ka`emo da je znatno asimetri~an. Kada je ñ3 jednako nuli, ka`emo da je raspored simetri~an.
MERE SPQO[TENOSTI RASPOREDA
Mere spqo{tenosti rasporeda su relativne mere kojima se ispituje spqo{tenost oblika rasporeda u zavisnosti od odnosa frekvencije sredwih vrednosti i frekvencija ostalih vrednosti obele`ja. Mera spqo{tenosti rasporeda se dobija po formuli:
Mera spqo{tenosti rasporeda ñ4 = M4 / ÃÂ4 |
Gde je M4 ~etvrti centralni momenat rasporeda, ÃÂ4 je standardna devijacija na ~etvrti stepen. Kao oznaka za meru asimetrije rasporeda koristi se gr~ko slovo ñ4 (koje se ~ita alfa ~etiri). ^etvrti stepeni se poni{tavaju i dobijamo relativnu meru. Raspored ima normalnu spqo{tenost ako je ñ4 jednako tri, ako je ñ4 mawe od tri, ka`emo da je raspored vi{e spqo{ten od normalnog rasporeda, a ako je ñ4 ve}e od tri, ka`emo da je raspored vi{e izdu`en od normalnog rasporeda.
PRIMER ZA PRIMENU MERA DESKRIPTIVNE ANALIZE
Dat nam je primer pregleda invalidskih penzija po mesecima 2002. godine za korisnika NN:
mesec | Iznos u din. |
Januar | 9000 |
Februar | 14511 |
Mart | 14593 |
April | 14663 |
Maj | 14716 |
Jun | 14836 |
Jul | 14852 |
Avgust | 14899 |
Septembar | 14940 |
Oktobar | 14982 |
Novembar | 15011 |
Decembar | 15010 |
Minitab 14.13 nam je dao slede}i izlaz:
Total
Variable Count Mean StDev Variance CoefVar Minimum Q1 Median Q3
C1 12 14334 1688 2849648 11,78 9000 14611 14844 14972
Variable Maximum Range IQR
C1 15011 6011 361
Obja{wewe dobijenih podataka : aritmeti~ka sredina posmatrane pojave iznosi 14334 (u Minitabu ozna~ava se sa Mean), varijansa je 2849648 (u Minitabu ozna~ava se sa Variance), standardna devijacija je 1688 (u Minitabu ozna~ava se sa StDev), koeficijent varijacije je 11.78% (u Minitabu ozna~ava se sa CoefVar), medijana je 14844 (u Minitabu ozna~ava se sa Median), prvi kvartil je 14611 (u Minitabu ozna~ava se sa Q1), tre}i kvartil je 14972 (u Minitabu ozna~ava se sa Q3), interkvartilna razlika je 361 (u Minitabu ozna~ava se sa IQR), interval varijacije je 6011 (u Minitabu se najbli`e obele`ava sa Range). U ovom primeru ne mo`e se izra~unati modus jer se svaka vrednost pojavquje samo jedanput. Po{to se u primeru nalazi ekstremna vrednost (za januar mesec iznos je 9000, vrednost koja dosta odstupa od ostalih vrednosti), aritmeti~ka sredina nije najboqi pokazateq sredwe vrednosti, ve} je medijana (na koju ne uti~u ekstremne vrednosti). Ekstremna vrednost povla~i raspored u levo, a po{to nam je medijana najboqa mera centralne tendencije, interkvartilna razlika nam je najboqa mera disperzije.
ZAKQU^AK
Kada se odlu~imo da posmatramo neku pojavu, moramo pa`qivo da se odlu~imo i kako }emo skupqati i sre|ivati podatke posmatrane pojave. Pored osobina pojave koju posmatramo, i materijalna strana istra`ivawa uti~e na odabir metoda (svaka studija naj~e{}e ima veoma ograni~en buxet). Statisti~ki popis je mnogo temeqniji, ali i izda{niji od statisti~kog uzorka. Statisti~ki uzorak prikupqen na ispravan na~in daje efikasnije podatke od statisti~kog popisa. Kada prikupimo i sredimo podatke (prema potrebama istra`ivawa zavisi da li }emo grupisati i na koliko grupa), biramo i koje mere deskriptivne analize }emo koristiti. Ako me|u posmatranim pojava nema ekstremnih vrednosti, onda nam je aritmeti~ka sredina najboqa sredwa vrednost koja }e pokazati karakteristike posmatrane pojave, kada pak ima ekstremnih vrednosti, odlu~i}emo se za medijanu. Zavisno od koje sredwe vrednosti smo se odlu~ili da nam najvi{e odgovara, uze}emo mere disperzije. Medijani najvi{e odgovara interkvartilna razlika, aritmeti~koj sredini najvi{e odgovara standardna devijacija.
�
SADR@AJ:
UVOD | 3 |
MERNE SKALE | 3 |
NOMINALNA SKALA | 3 |
ORDINALNA SKALA | 3 |
INTERVALNA SKALA | 4 |
SKALA ODNOSA | 4 |
METODI PRIKUPQAWA PODATAKA | 4 |
STATISTI^KI POPIS | 4 |
STATISTI^KI IZVE[TAJ | 4 |
STATISTI^KI UZORAK | 4 |
SRE\IVAWE I OBRADA PODATAKA | 5 |
PRIKAZIVAWE PODATAKA | 5 |
SERIJE STRUKTURE | 5 |
VREMENSKE SERIJE | 6 |
TABELARNO PRIKAZIVAWE | 7 |
GRAFI^KO PRIKAZIVAWE | 8 |
GRAFI^KO PRIKAZIVAWE U PRAVOUGLOM KOORDINATNOM SISTEMU | 8 |
GRAFI^KO PRIKAZIVAWE NUMERI^KIH SERIJA SA PREKIDNIM OBELE@JEM | 8 |
GRAFI^KO PRIKAZIVAWE NUMERI^KIH SERIJA SA NEPREKIDNIM OBELE@JEM | 9 |
GRAFI^KO PRIKAZIVAWE VREMENSKIH SERIJA | 11 |
GRAFI^KO PRIKAZIVAWE U POLARNOM KOORDINATNOM SISTEMU | 12 |
GRAFI^KO PRIKAZIVAWE VAN KOORDINATNOG SISTEMA | 12 |
DESKRIPTIVNE MERE | 13 |
MERE CENTRALNE TENDENCIJE | 14 |
ARITMETI^KA SREDINA | 14 |
GEOMETRIJSKA SREDINA | 15 |
HARMONIJSKA SREDINA | 15 |
MODUS | 16 |
MEDIJANA | 16 |
MERE DISPERZIJE | 17 |
INTERVAL VARIJACIJE | 17 |
INTERKVARTILNA RAZLIKA | 17 |
SREDWE APSOLUTNO ODSTUPAWE | 17 |
VARIJANSA | 18 |
STANDARDNA DEVIJACIJA | 18 |
KOEFICIJENT VARIJACIJE | 18 |
KOEFICIJENT INTERKVARTILNE VARIJACIJE | 18 |
STANDARDIZOVANO ODSTUPAWE | 19 |
MERE OBLIKA RASPOREDA | 19 |
MERE ASIMETRIJE RASPOREDA | 19 |
MERE SPQO[TENOSTI RASPOREDA | 19 |
PRIMER ZA PRIMENU MERA DESKRIPTIVNE ANALIZE | 20 |
OBJA[WEWE DOBIJENIH PODATAKA | 21 |
ZAKQU^AK | 21 |
ENDNOTE | 22 |
LITERATURA | 23 |
�
Endnote:
@i`i} M, Lovri} M, Pavli~i} D, METODI STATISTI^KE ANALIZE, Beograd: centar za izdava~ku delatnost Ekonomskog fakulteta, 2005. (str. 11)
isto (str.15)
Human Development Report, Oxford University Press, 1999. (32.str)
@i`i} M, Lovri} M, Pavli~i} D, METODI STATISTI^KE ANALIZE, Beograd: centar za izdava~ku delatnost Ekonomskog fakulteta, 2005. (str. 22)
Hearts of Iron, Paradox, 2005. (1.str)
@i`i} M, Lovri} M, Pavli~i} D, METODI STATISTI^KE ANALIZE, Beograd: centar za izdava~ku delatnost Ekonomskog fakulteta, 2005. (str. 38)
�
LITERATURA KORI[]ENA PRI IZRADI PRISTUPNOG RADA:
OSNOVNA LITERATURA:
@i`i} M, Lovri} M, Pavli~i} D, METODI STATISTI^KE ANALIZE, Beograd: centar za izdava~ku delatnost Ekonomskog fakulteta, 2005.
DODATNA LITRATURA:
HELP FILE IZ MINITABA 14.13
STRANICE SA INTERNETA
PRI IZRADI PRISTUPNOG RADA KORI[]EN JE STATISTI^KI PAKET MINITAB 14.13
SVI PRIMERI (SEM AKO NIJE NAVEDENO DRUGA^IJE) SU POTPUNO PROIZVOQNI I DELO SU AUTORA OVOG RADA. SVAKO POKLAPAWE SA NE^IJIM TU\IM PRIMERIMA JE POTPUNO NENAMERNO