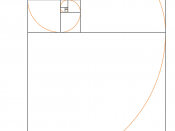
The Golden Section
The Golden Section has been referred to as the Divine Proportion, the golden ratio or the Golden Rectangle. This proportion has been demonstrated in the Greek architecture of the Parthenon, the Renaissance architecture of Leon Battista Alberti's Santa Maria Novella in Florence, in the Invisible Squares of Mondrian and used extensively by Le Corbusier in his quest for modular designs of modern architecture.
To make the golden section you must:
Step 1: Draw a square. (Make sure all the sides are equal)
Step 2: Draw a line from the right of the square to the opposite corner; construct an arc that will define the extents of the new rectangle.
Step 3: Using the endpoints of the arc, complete the rectangle.
Step 4: This ratio (1:1.618) is known as the golden rectangle.
The ancient Greeks used the golden section in their art and architecture. Apparently, many ancient buildings use golden rectangles.
The ancient Greeks thought that this was the most pleasing of all rectangles. It was not too thick, not too thin, but just right, the perfect shape for creating buildings. In the 4th century B.C Plato was establishing study on this rectangle. The grate mathematician Luca Pacioli wrote a book about the golden section and was illustrated with 60 drawings by Leonardo da Vinci
The golden section is seen in many areas of mathematics. The ratio is of consecutive Fibonacci numbers 1, 1, 2, 3, 5, 8, 13 . . ., each number being the sum of the previous two numbers. The golden section shows up as an exact fit in mathematics in many unexpected places. The ratio shows up everywhere in the five-pointed star and in the pentagon.
Another piece of the mathematical wonder is that the rectangle may be subdivided into more of...