A function is a relation in which each element of the domain is paired with exactly one element in the range. Two types of functions are the exponential functions and the logarithmic functions. Exponential functions are the functions in the form of y = ax, where ''a'' is a positive real number, greater than zero and not equal to one. Logarithmic functions are the inverse of exponential functions, y = loga x, where ''a'' is greater to zero and not equal to one. These functions have certain differences as well as similarities between them. Also they are very useful for various situations in life.
Logarithmic functions are fairly different from the exponential functions. The first difference that we can find between them is in the equations, they are inverse to each other. The logarithmic equation is y = loga x and the exponential equation is y = ax. We can also see that the natural exponential function is different form the natural logarithmic function.
F(x)=e**(k*x)
F(x)=a**x
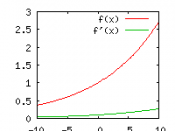
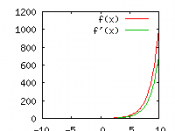
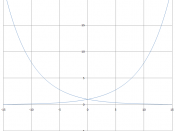
English: Symmetric exponential functions ΕλληÎ...The natural exponential function is y = f(x) = ex and the natural logarithmic function is f(x) = loge x = lnx , where x > 0. Also we can see that to graph and exponential function it always has to pass through the point (0,1).
However, both of these functions also have similarities. Both of the functions contain an ''a'' which has to be greater than zero and less than one. Also when we graph both of the functions we can see that they will never touch an axis because of the rule that ''a'' is greater than zero and less than one. To solve exponential functions, you use the same rules set of rules that you use to solve logarithmic functions. (logamn = loga m + loga n, logam / n = loga m...