� PAGE �2�
The Fractal Coastline:
An example of a natural fractal
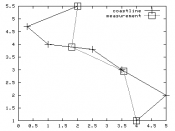
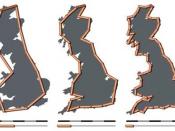
How is measuring the length of a coastline different from measuring the circumference of a circle or the distance around a square? For example: How long is the coastline along an ocean shore? Is its length equal to the mileage reading on the odometer of an automobile driving along the straight road beside the beach? Is it the distance covered by a bicyclist who pedals along the shore on a footpath? Is it the length run by a jogger whose morning exercise includes running ''next to the water?'' Whose ''length of coastline'' is the true one? Trying to answer these innocent questions leads to deeper questions and our first look at natural fractals.
Coastlines are examples of natural fractals, also called random fractals. Natural fractals are formed through random processes, such as erosion of a beach to create coastlines.
Figure 1
The coastline of the United Kingdom as measured wi...
H fractal. Its fractal dimension equals 2.No two coastlines are ever exactly the same; neither are two snowflakes or two lightning bolts. Though two such patterns may have some overall features in common, if you look closely you will see that they differ in the details of their structure. The same is true for other natural fractals as well. Each example is unique, because the chances are almost zero that exactly the same sequence of random events will occur in the growth of two different patterns, such as two snowflakes. The erosion process on a beach is random: the resistance of rocks along the shore as well as the force of incoming waves at a particular spot vary more or less randomly.
Mandelbrot was the first to publish anything about fractals and their correlation to coastlines. He discussed that they have a Hausdorff dimension between 1 and 2. This means that they lie...