Fractions are ways to represent parts of a whole. Common fractions are ý and þ. These are proper or regular fractions. Some fractions are called mixed numbers. These are represented by a whole number with a fraction (proper fraction). 1 ý and 2 þ are good examples. An improper fraction has a larger number on the top than on the bottom, such as 9/8. I will explain how to convert these fractions to decimals. I will show you how to change an improper fraction to a mixed number. Operations (addition, subtraction, multiplication, and division) will be explained as well.
CONVERSIONS
This section will explain how to convert a fraction into a decimal. First, let's get an example fraction. How about 3/8? To find a decimal, divide the numerator (top number) by the denominator (bottom number). So we would divide 3 by 8. 3)8=0.375 or .38. Lets do another.
Try 1/3. 1)3=.33333... So 1/3 is equal to about.33.
Next comes the mixed numbers to the improper fractions . All you do is multiply the denominator by the whole number and add the numerator. This is the numerator of the improper fraction. You keep the same denominator. Let's try 2þ. Four times two is eight. Eight plus three is eleven. Keep the denominator and you have 11/4. Now to convert the improper fraction into a mixed number. You need to remember, keep the same denominator. 9/2=4ý. 2 goes into 9 4 times. There is 1 left over. So, it equals 4ý.
OPERATIONS
First, I will explain how to add like fractions, then, unlike fractions. Let's say you have þ of a pizza and ü of a pizza. How much pizza do you have? When adding fractions, you NEVER add the denominators. Just the...


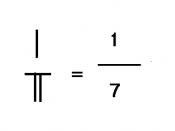
Nice lesson plan
nice way to intoduce youngsters to the exciting world of fractions
10 out of 10 people found this comment useful.