Fractions

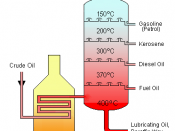
Mine is not to reason why, I just invert and multiply.

There is ample evidence that children find the learning of fractions a major difficulty (Behr, Harel, Post, & Lesh,1992; Davydov & Tsvetkovich,1991; Hiebert & Behr,1988; Kieren,1976; Mack,1990; McLellan & Dewey, 1908: Cited in Tzur, 1999: Van de Walle, 1990: Behr, Harel, Post, & Lesh; Hunting, Davis, & Pearn, 1996; Mack, 1995: Cited by Thompson, & Saldanha, 2003). Students’ have many misconceptions about fractions including the belief that the fraction having the larger denominator is always larger, two fractions that are almost equal are equivalent (Johnson, 1998; Mack, 1990), fractions are parts of shapes, fractions are never bigger than 1 and that fractions are not numbers in their own right (Mack, 1990). Many students’ have trouble interpreting mixed numbers (Kouba, 1988a; cited by Van de Walle, 2007: Ball, 1990; As cited in Tsao, 2005) and suffer confusion with the meaning of operations and rules learnt (Mack, 1995: Ball, 1990; As cited by Tsao, 2005).

Diagram drawn by Theresa knott. This is a diagram ...

Ford circles. A circle rests upon each fraction in...

English: display showing fractions.

Research also shows that although some students’ may be fairly capable of working with fractional computations they don’t really understand what fractions are (Kouba, Zawojewski, and Strutchens, 1997).

Often children come into the classroom with a basic understanding of fractions through sharing (Mack, 1990), particularly when performing operations on fractions using real-life situations (Gunderson & Gunderson, 1957; Leinhardt, 1988: as cited by Mack, 1990). This gives a strong base for teachers’ to help students construct the idea of fractional parts of a whole and the outcome of sharing in equal parts through the acting out of story based problems such as sharing lollies or biscuits among a varying number of students’ (Van de Walle, 2007). It is very important to introduce the vocabulary of fractional language which can be done quite casually using terms such as...