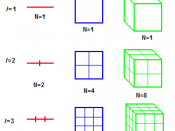
The Fun Filled Fractal Phenomenon A fractal is a type of geometric figure. It is generated by starting with a very simple pattern such as a triangle and, through the application of many repeated rules, adding to the figure to make it more complicated. Often, an input will be entered into a recursive function and it will yield an output. This output is then inserted back into the function as an input and the process is repeated infinitely. Fractals often exhibit self-similarity. This means that each small section of the fractal can be viewed as a reduced-scale replica of the whole. Some famous fractals include Sierpinski's triangle, Koch's snowflake and the length of a coastline. Fractals were brought to the public's attention by the work of French mathematician Benoit B. Mandelbrot in the 1970's. Mandelbrot discovered how to calculate fractal dimensions. The formula for fractal dimension is N=2D where N equals the number of copies of the original figure, which is calculated by doubling its size and D is the dimension.
The first 3 iterations of the type 2 quadratic Koc...
Fractals Geometric Pattern
English: Aid to defining fractal dimensionsMandelbrot named his creations fractals because each part is a fraction of the whole figure.
The Chaos Theory describes the complex and unpredictable motion of systems that are sensitive to their initial conditions. Chaotic systems follow precise laws but their irregular behavior can appear to be random to the casual observer. For example, weather is a chaotic system. If the rays of the sun bounce off the hood of a car in a certain way, causing a breeze, the breeze could blow a leave off a tree, which starts a series of additional events that could alter the weather in some other part of the world. Chaos can be related to fractals. In a fractal if one tiny change occurs in a repeated pattern, the entire fractal will change.