Group Theory and the Rubik's Cube

In abstract mathematics, a very large topic is the concept of a group. This is studied in Group Theory, which at a mathematical level is the study of symmetry in a very abstract way (groups usually manifest themselves in nature in forms of symmetry) [5]. Recently, there have been various breakthroughs in group theory, such as the Classification of Finite Simple Groups (the longest mathematical proof) [7], and the three-hundred page proof that all odd-ordered groups are solvable, which won the Abel prize [6].

A group is a set of objects, called elements, that, when paired with an operation •, satisfy three axioms: closure (for all elements a and b in the set, a•b is also in the set), associativity (for all three elements a, b, and c, a•(b•c)=(a•b) •c), existence of an identity (there exists an element e such that for all elements a, e•a=a•e=a) and existence of inverses (for all elements a, there exists an element a-1 such that a•a-1=e).

English: A sketch of a standard Cayley graph of th...

From the availability heuristic to Cayley's Theore...

Rubik's cube on the tracks

From these axioms, a few simple consequences arise, and group theory is the study of these consequences [5].

Here is an example of a group (this group is known as the dihedral group). If we take a triangle, we can create a group with three elements. If we set the element e as the element that does nothing to the triangle, e would be the identity. We can then say that α is the element that turns the triangle 120° clockwise and α2 turns the triangle 240° clockwise. This set – {e, α, α2} – is associative, has closure, has an identity, and has inverses. One thing that should be mentioned, because it will be useful in the future, is the idea of a generator. If we say that e=α0, then we can say that all elements in the group can be represented as a power of α. This means that α is a generator of the group. The more complex groups can have many generators [8].

The last axiom, the existence of inverses, has caused problems in groups, because in some groups the inverse is not immediately obvious. One good example of such a group is the Rubik’s cube group, and the fact that its identities aren’t immediately obvious is shown in the difficulty of solving it. Each element of the group, which is each combination, has an inverse, or a way of solving it, and this inverse has a certain number of steps. The number of steps required for the quickest inverse of the most solved state of the cube, which in group theory terms is the diameter of the group, has been a standing conjecture ever since the Rubik’s cube was created – over 25 years ago. This number has been called God’s number, the idea being that an omnipresent being would know the optimal step for any given configuration. When the idea was started, the upper bound of the number was set at 52, and the lower bound has been set to 18. These bounds have been improved to a lower bound of 20 and an upper bound of 26. The latest improvement was achieved by Daniel Kunkle and Gene Cooperman at Northeastern University in Boston [1].

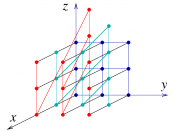
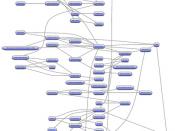
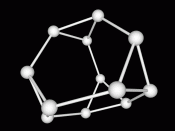
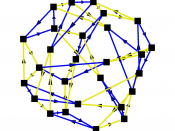
The diameter of a group could be defined as the number of moves in the best possible solution in the worst possible case, but it is usually paired with the Cayley graph of the group. The Cayley graph is composed of vertices and edges. Each vertex is an element of the group, and each edge is an operation of the element and another element from a predetermined subset of the group (usually the set of generators). With this, the group can be understood a lot easier. A second recent achievement in the field of combination puzzles and group theory is the creation of a Cayley graph for the 2×2×2 cube [4].

Bibliography:1.Cooperman, Gene and Daniel Kunkle. (2007). Twenty-Six Moves Suffice for Rubik’s Cube. Retrieved 27 December, 2007 from http://www.ccs.neu.edu/home/gene/papers/rubik.pdf.

2. (2007). Rubik’s Cube group – Wikipedia, the free encyclopedia. Retrieved 7 February, 2008 from http://en.wikipedia.org/wiki/Rubik%27s_Cube_group.

3.Joyner, David. Adventures in Group Theory. Baltimore: Johns Hopkins University Press (2002).

4.Cooperman, G., L. Finklestein, and N. Sarawagi. "Applications of Cayley Graphs." Appl. Algebra, Alg. Algo. and Error Correcting Codes . College of Computer Science, Boston. 1990.

5.(2007). Group Theory - WIkipedia, the free encyclopedia. Retrieved 10 February, 2008 from http://en.wikipedia.org/wiki/Group_theory.

6.Feit, Walter and John Griggs Thompson. "Solvability of Groups with Odd Order." Pacific Journal of Mathematics. Fall 1963.

7.(2007). Classification of Finite Simple Groups - Wikipedia, the free encyclopedia. Retrieved 9 February, 2008 from http://en.wikipedia.org/wiki/Classification_of_finite_simple_groups.

8.(2007). Generating set of a group - Wikipedia, the free encyclopedia. Retrieved 8 February from http://en.wikipedia.org/wiki/Generating_set_of_a_group.

Rubik's Cube Collection

A rendering of a truncated tetrahedron network (th...

English: The Cayley graph of the free Burnside gro...