When the allele frequencies in a population remain constant from generation to generation, the population is said to be in Hardy-Weinberg equilibrium where there is no evolution. Such conditions are when there is a very large population size, no migration, no net mutations, random mating, and no natural selection.
In a very large population, genetic drift, which is the change in a population's allele frequencies due to chance, can cause genotype frequencies to change over time.
When there is no migration, and gene flow, the transfer of alleles between populations due to the movement of individuals or gametes, occur, the frequency of any genotype that is in high frequency among the immigrants increase.
When there is no net mutations, by changing on allele into another, mutations change the gene pool.
When random mating occurs with certain genotypes, then the random mixing of gametes required for Hardy-Weinberg equilibrium does not occur.
Hardy-Weinberg principle
Allele - 02/28/06 Cleveland, OH
Allele - 02/28/06 Cleveland, OHWhen there is no natural selection change in frequencies may occur due to different survival and reproductive success of genotypes and may result in different frequencies than the predicted frequencies by the Hardy-Weinberg equation.
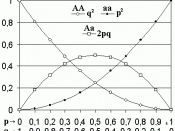
Hardy-Weinberg equilibrium is determined by evaluating the allele frequencies for each allele (p and q), frequency of homozygotes (p2 and q2), and the frequency of heterozygotes (2pq); and also the two equations, that indicate that all alleles sum to 100% (p+q=1) and that all individuals sum to 100% (p2+2pq+q2=1) Below is the work shown to calculate the frequencies of a rabbit population that consists of 100,000 rabbits of which 25,000 are white and 75,000 are agouti.
If 25,000 rabbits are white then 25,000/100,000=q2
So 0.25=q2
Route 0.25=q
0.5=q
Since p+q=1
Then 1-q=p
So 1-0.5=0.5
Thus p=0.5
And p2=(0.5)(0.5)=0.25
Now we know 2(0.5)(0.5)=2pq
p2=homozygous dominant frequency=0.25
q2=recessive allele frequency=0.25
2pq=heterozygous frequency=0.5