Continuous Random Variables

A random variable whose values are not countable is called a continuous random variable.

The Normal Distribution

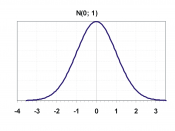
The normal probability distribution is given by a bell-shaped(symmetric) curve.

The Standard Normal Distribution

The normal distribution with

Example 1: Find the area under the standard normal curve

between z = 0 and z = 1.95

from z = -2.17 to z = 0

Area to the right of z = 2.32

Area to the left of z = -1.54

Example 2a: Find the following probabilities for the standard normal curve.

(a)

Example 2b: Find the value of k if

(a)

Standardizing A Normal Distribution

Example 3: Let x be a normal random variable with its mean equal to 40 and standard deviation equal to 5. Find the following probabilities for this normal distribution.

Standard deviation illustration

curve of standard normal distribution, empty

English: A plot of the Q-function, the tail probab...

(a)

(b)

(c)

(d)

Example 4: Lengths of metal strips produced by a machine are normally distributed with mean length of 150cm and a standard deviation of 10cm.

Find the probability that the length of a randomly selected strip is

(a) shorter than 165cm,

(b) within 5cm of the mean.

Example 5: The time taken by the milkman to deliver to the High Street is normally distributed with a mean of 12 minutes and a standard deviation of 2 minutes. He delivers milk every day. Estimate the number of days during the year when he takes

(a) longer than 17 minutes,

(b) less than ten minutes,

(c) between 9 and 13 minutes.

Example 6: The height of female students at a particular college are normally distributed with a mean of 169cm and a standard deviation of 9 cm.

(a) Given that 80% of these female students have a height less...