1.1 Introduction
This "book" is not intended to be a vast, definitive treatment of everything that is known
about geometric optics. It covers, rather, the geometric optics of first-year students,
whom it will either help or confuse yet further, though I hope the former. The part of
geometric optics that often causes the most difficulty, particularly in getting the right
answer for homework or examination problems, is the vexing matter of sign conventions
in lens and mirror calculations. It seems that no matter how hard we try, we always get
the sign wrong! This aspect will be dealt with in Chapter 2. The present chapter deals
with simpler matters, namely reflection and refraction at a plane surface, except for a
brief foray into the geometry of the rainbow. The rainbow, of course, involves refraction
by a spherical drop. For the calculation of the radius of the bow, only Snell's law is
needed, but some knowledge of physical optics will be needed for a fuller understanding
of some of the material in section 1.7,
English: Illustration of wavefronts in the context...
Ray Diagram 2
Refraction #7which is a little more demanding than the rest of
the chapter.
1.2 Reflection at a Plane Surface
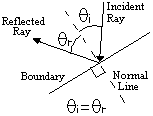
The law of reflection of light is merely that the angle of reflection r is equal to the angle
of incidence r. There is really very little that can be said about this, but I'll try and say
what little need be said.
i. It is customary to measure the angles of incidence and reflection from the normal to
the reflecting surface rather than from the surface itself.
i r
FIGURE I.1
2
ii. Some curmudgeonly professors may ask for the lawS of reflection, and will give you
only half marks if you neglect to add that the incident ray, the reflected ray and the
normal are coplanar.