Until the sixth century BC, there were people shrouded in mystery. Living in the area
east of the Mesopotamian region, the Persians were a disparate group of
Indo-European tribes, some nomadic, some settled, that were developing their own
culture and religion unique from that of the great cities to their west. The Persians
throughout their history, such as we know it, lived peacefully in the region just north
of the Persian Gulf (modern day Iran).
Persia was also famous for its research in maths. Many important
mathematicians and especially mathematical astronomers lived and worked in Persia.
Mathematicians in Persia often discovered mathematical principles many centuries
before mathematicians in Europe did. They were also the first people to read what the
ancient Greeks had said about maths and to copy it and pass it on later to Europeans.
Persians also made many very beautiful mathematical and astronomical instruments,
especially astrolabes. The Persians were mathematically endowed and were able to
solve things that we are not able to solve today.
They used such concepts as the
Pascal's Triangle. They revised the quadratic equation and introduced the algorithm.
Among others was the hypocycloid.
Pascal's triangle is named after the French mathematician and philosopher
Blaise Pascal, who wrote a Treatise on the Arithmetical Triangle describing it. But
Pascal was not the first to draw out this triangle or to notice its amazing properties!
Long before Pascal, 10th century Indian mathematicians described this array of
numbers as useful for representing the number of combinations of short and long
sounds in poetic meters. The triangle also appears in the writings of Omar Khayyam,
the great eleventh-century astronomer, poet, philosopher, and mathematician, who
lived in what is modern-day Iran.
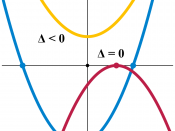
A Quadratic Equation is a polynomial equation in which the highest power of
the unknown variable is 2.