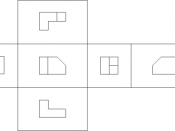
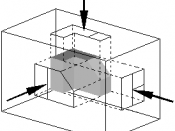
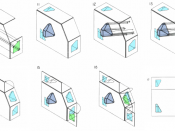
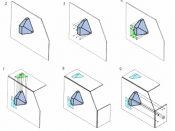
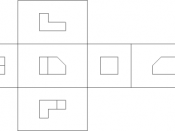
Orthographic projection The technique of orthographic projection is a method of representing three-dimensional objects by three two dimensional drawings, in each of which the object is viewed along parallel lines that are perpendicular to the plane of the plane of the drawing. For example an orthographic projection of a house typically consists of a plan view, a front view and a side view. There are a number of reasons for why the use of orthographic drawings is beneficial.
Orthographic projection the solution to the biggest problem that a draughtsman has to solve, This how to draw with sufficient clarity, a three dimensional object on a two dimensional piece of paper. The drawing must show quite clearly the detailed outlines of all of all the faces and their outlines must be fully dimensioned. In the case of simple objects this can be achieved by being drawn in either an isometric or oblique projection, but these methods have disadvantages in that circles and curves are difficult to draw.
An example of a multiview orthographic drawing fro...
Views of object shown according to third-angle pro...
Views of an object being projected according to th...Also neither show more than three sides of an object in any one view. Orthographic projection, because of its flexibility in allowing any number of views of the same object does not present such drawbacks. Another advantage of orthographic drawings is that all facets of a form parallel to the drawing surface are represented without foreshortening. Therefore the true size, shape and proportion are retained.
There are two forms of showing orthographic projection, The first angle and the third angle. In these projections the projectors are parallel to the picture. Orthographic projection presents a true picture of each of each face of an object; circles remain as circles and ellipses remain as ellipses. Horizontal lines remain as horizontal lines and vertical lines remain vertical. There is no limit to the number of views that can be drawn: If the object that you wish to draw is complicated, it is possible to show half a dozen views; if it is simple two will suffice. No matter how many views are drawn, they all related to each other in position.
Figures ten through seventeen.
Figures one through nine.
Image showing orthographic views located relative ...