Chapter 6 Outline
Identify distributions as symmetrical or skewed.
Identify the properties of the normal distribution.
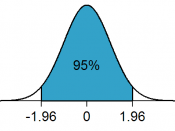
Find the area under the standard normal distribution, given various z values.
Find the probabilities for a normally distributed variable by transforming it into a standard normal variable.
Find specific data values for given percentages using the standard normal distribution.
Use the central limit theorem to solve problems involving sample means for large samples.
Use the normal approximation to compute probabilities for a binomial variable.
Introduction
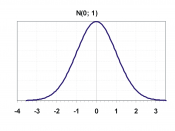
Many continuous variables have distributions that are bell-shaped and are called approximately normally distributed variables.
A normal distribution is also known as the bell curve or the Gaussian distribution.
Normal and Skewed Distributions
The normal distribution is a continuous, bell-shaped distribution of a variable.
If the data values are evenly distributed about the mean, the distribution is said to be symmetrical.
If the majority of the data values fall to the left or right of the mean, the distribution is said to be skewed.
curve of standard normal distribution, empty
English: A plot of the Q-function, the tail probab...
Standard normal distribution shading area between ...Left Skewed Distributions
When the majority of the data values fall to the right of the mean, the distribution is said to be negatively or left skewed. The mean is to the left of the median, and the mean and the median are to the left of the mode.
Right Skewed Distributions
When the majority of the data values fall to the left of the mean, the distribution is said to be positively or right skewed. The mean falls to the right of the median and both the mean and the median fall to the right of the mode.
Equation for a Normal Distribution
The mathematical equation for the normal distribution is:
Properties of the Normal Distribution
The shape and position of the normal distribution curve depend on two parameters, the mean and the...