Introduction Modern physics and philosophy both share their origin in ancient Greece, where there was little or no distinction made between them. At that point in time, both Physics and Philosophy were purely intellectual exercises of logic; conclusions drawn through physical investigation were seen to be less 'pure' than conclusions based on logic.
Much of physics is now based on empirical data, and this data is required for any theory to be accepted by the scientific community. This expansion into empirical research can be seen as the sole reason physics has become more advanced (and therefore more powerful as a mental tool). Philosophy has never moved into specific empirical research in the same way, and so is free to criticise the logic of empirical research. The purpose of this essay is to explain these criticisms, including the problem of induction, the problem of probability and problems with the system of perception.
David Hume's statements on ethics foreshadowed tho...
English: inductive and deductive reasoning
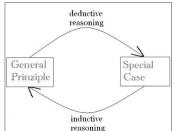
Worthy Of Note: The Sacred Suspicion of Truth and ...The effects and validity of these criticisms of empirical research will be shown through logic and historical example. In conclusion I intend to show ultimately the validity of these criticisms depend on the individuals view of the purpose of physics; is it a useful system of thought which allows us to usefully manipulate physical systems? Alternatively, is physics a method of describing the actuality of the physical universe? The Problem of Induction To understand the problem of induction we must first understand 'traditional' logic. 'Traditional' logic will be defined for our purposes as deductive logic. In the deductive process, inference leads from a specific set of premises to a conclusion just a certain as the premises. This means that the conclusion draw from the facts in a specific circumstance is equally valid logically, as the validity of those facts.
Inductive logic is defined as 'general inference from particular instances'[1].