Platonic Solids Essay- This is an essay i wrote for math class on why there are exactly five regular polyhedra, and why there can never be any more of them.

Platonic Solids Essay

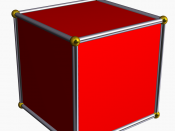
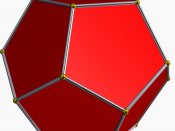
I think that there are exactly five regular polyhedra, and I intend to prove why there are exactly five polyhedra. Ok, firstly, we need to identify what the five polyhedra are. They are the tetrahedron, the cube, the octahedron, the icosahedron, and the dodecahedron. All of these are regular polyhedra have something in common. For each shape, each of its faces are the same regular polygon, and the same number of faces meet at a vertex. This is the rule for forming regular polyhedra. Now we need to analyze the shapes of the faces, and the number of them meeting at a vertex. The faces for the tetrahedron, octahedron, and the icosahedron are all triangles, and the number of faces meeting at a vertex is 3, 4, and 5 respectively. The faces in a cube are all squares, and the number of faces meeting at a vertex is 3.

Image d'un cube

Image d'un dodécaèdre

A Hexahedron (cube). A regular polyhedron. Created...

Finally, for the dodecahedron, there are 3 pentagons meeting at each vertex.

The key observation is that the interior angles of the polygons meeting at a vertex of a polyhedron add up to less than 360 degrees. This is the key element in making sure if the conditions for constructing a polyhedron hold true. Now we must analyze the shapes and see which ones can make a regular polyhedron. For any shape, you cannot use less than 3 faces meeting at a vertex because it is impossible to create a closed 3-D figure with less than 3 faces meeting at a vertex. So we can rule that out for each shape. For a triangle, since the angles are 60 degrees each, you can have 3, 4, and 5 faces meeting at a vertex without the angular defect being 360 or more, and all of those are polyhedra I...