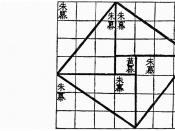
Plimpton 322 is a cuneiform clay tablet with the catalog number 322 in the G.A. Plimpton Collection at Columbia University. Probably the most well known mathematical tablet, it was written in the Old Babylonian period between 1900 and 1600 B.C.E. and shows the most advanced mathematics known before the development of the Greek mathematics. It was originally thought that Plimpton 322 was one of many tablets that recorded inventories of food and merchandise. However, in 1946 Otto Neugebauer and A. J. Sachs, historians of mathematics, discovered that the numbers in the table were computations and not just records of quantity.
Plimpton 322 is written sexigesimally (in base 60) with combinations of two symbols, one for tens and one for units. There are fifteen rows and four columns on the tablet. There may have been more columns in the portion of the tablet that broke off. The last column is the row number.
Visual proof of the Pythagorean theorem for the (3...
English: Animated geometric proof of the Pythagora...
Saarbrücken, HTW, Mathematics WorkshopThe second, third and fifth columns are headed by words interpreted to mean "width", "diagonal" and "name", respectively. The tablet is often converted to decimal form, although it is not clear whether the numbers are fractions or integers.
The first column of Plimpton 322 is interesting because each number is a perfect square and subtracting one from each leaves a perfect square. This table is usually related to Pythagorean triples. In interpreting it, the second column is considered a, one side of a right triangle or the width of a rectangle. The third column is considered c, the hypotenuse of the right triangle or the diagonal of the rectangle. The other side of the triangle or rectangle, b, does not appear on the table. In this interpretation the first column is then (c/b)2 = 1 + (a/b)2 . Neugebauer and Sachs confirmed that the columns were computations...