Pythagroas triples.

My formulas are

1.2n + 1

2.2n2 + 2n

3.2n2 + 2n + 1

4.4n2 + 6n + 2

5.2n3 + 3n2 + n

To get these formulas I did the following

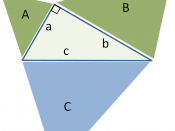
1.Take side 'a' for the first five terms 3, 5, 7, 9, 11. From these numbers you can see that the formula is 2n + 1 because these are consecutive odd numbers (2n + 1 is the general formula for consecutive odd numbers) You may be able to see the formula if you draw a graph

2.From looking at my table of results, I noticed that 'an + n = b'. So I took my formula for 'a' (2n + 1) multiplied it by 'n' to get '2n2 + n'. I then added my other 'n' to get '2n2 + 2n'. This is a parabola as you can see from the equation and also the graph

English: Scatter plot of the legs (a,b) of the fir...

English: a plot of the first 47 PPTs. vi:Hình:P...

English: Pythagoras' theorem applied to similar tr...

3.Side 'c' is just the formula for side 'b' +1

4.The perimeter = a + b + c. Therefore I took my formula for 'a' (2n + 1), my formula for 'b' (2n2 + 2n) and my formula for 'c' (2n2 + 2n + 1). I then did the following: -

2n + 1 + 2n2 + 2n + 2n2 + 2n + 1 = perimeter

Rearranges to equal

4n2 + 6n + 2 = perimeter

5.The area = (a x b) divided by 2. Therefore I took my formula for 'a' (2n + 1) and my formula for 'b' (2n2 + 2n). I then did the following: -

(2n + 1)(2n2 + 2n) = area

2

Multiply this out to get

4n3 + 6n2 + 2n = area

2

Then divide 4n3 + 6n2 + 2n by 2 to get

2n3 + 3n2 + n

To prove my formulas for 'a', 'b' and 'c' are correct. I decided incorporate my formulas into a2 + b2 = c2: -

a2 + b2= c2

(2n + 1)2+ (2n2 + 2n)2= (2n2 + 2n + 1)2

(2n + 1)(2n + 1) + (2n2 + 2n)(2n2 + 2n) = (2n2 + 2n + 1)(2n2 + 2n + 1)

4n2 + 2n + 2n + 1 + 4n4 + 4n2 + 4n3 + 4n3= 4n4 + 8n3 + 8n2 + 4n + 1

4n2 + 4n + 1 + 4n4 + 8n3 + 4n2= 4n4 + 8n3 + 8n2 + 4n + 1

4n4 + 8n3 + 8n2 + 4n + 1 = 4n4 + 8n3 + 8n2 + 4n + 1

This proves that my 'a', 'b' and 'c' formulas are correct

Extension

Polynomials

Here are the formulas for the perimeter and the area

Perimeter = 4n2 + 6n + 2

Area = 2n3 + 3n2 + n

From my table of results I know that the perimeter = area at term number 2. Therefore

(n-2) is my factor

I would like to find out at what other places (if any) the perimeter is equal to the area

To find this out I have been to the library and looked at some A-level textbooks and learnt 'Polynomials'

4n2 + 6n + 2 = 2n3 + 3n2 + n

6n + 2 = 2n3 - n2 + n

2 = 2n3 - n2 - 5n

0 = 2n3 - n2 - 5n - 2

2n2 + 3n + 1 b

n - 2 ) 2n3 - n2 - 5n - 2

2n3 - 4n2 b

3n2 - 5n - 2

3n2 - 6n b

n - 2

n - 2 b

0

This tells us that the only term where the perimeter = area is term number 2

Therefore when f(x) = 2n3 - n2 - 5n - 2 is divided by n - 2 there is no remainder and a quotient 2n2 + 3n + 1. The result can be written as

f(x) = 2n3 - n2 - 5n - 2= (n - 2)(2n2 + 3n + 1)

If 2 was substituted for the x in this identity so that n - 2 = 0, the quotient is eliminated giving f (2) = + 2

Now I will complete the square on '4n2 + 6n + 2' to see what the solution to this is.

4n2 + 6n + 2

4(n +3)2 - 9 + 2

4(n +3)2 - 7

4(n +3)2 = 7

(n +3)2 = 1.75

n + 3 = 1.322875656

n + 3 = -1.322875656

n = -1.677124344

n = -4.322875656

Arithmatic Progression

I would like to know whether or not the Pythagorean triple 3,4,5 is the basis of all triples just some of them.

To find this out I have been to the library and looked at some A-level textbooks and learnt 'Arithmatic Progression'

3, 4, 5 is a Pythagorean triple

The pattern is plus one

If a = 3 and d = difference (which is +1) then

3 = a

4 = a + d

5 = a +2d

a, a +d, a + 2d

Therefore if you incorporate this into Pythagoras theorem

a2 + (a + d)2 = (a + 2d)2

a2 + (a + d)(a + d) = (a + 2d)2

a2 + a2 + ad + ad + d2 = (a + 2d)2

2a2 + 2ad + d2 = (a + 2d)2

2a2 + 2ad + d2 = (a + 2d)(a + 2d)

2a2 + 2ad + d2 = a2 + 2ad + 2ad + 4d2

2a2 + 2ad + d2 = 4d2 + a2 + 4ad

If you equate these equations to 0 you get

a2 - 3d2 - 2ad = 0

Change a to x

x2 - 3d2 - 2dx = 0

Factorise this equation to get

(x + d)(x - 3d)

Therefore

x = -d

x = 3d

x = -d is impossible as you cannot have a negative dimension

a, a+d, a + 2d

Is the same as

3d, 4d, 5d

This tells us that the only Pythagorean triples are 3, 4, 5 or multiples of 3, 4, 5 e.g. 6, 8, 10 or 12, 16, 20 etc.