SHIFTS IN A GRAPH There are three possible shifts in a graph. A shift is a transformation that moves a graph up or down (vertical) and left or right (horizontal). There is vertical shrinking or vertical stretching, horizontal shifts, and vertical shifts that are possible for a graph.
Vertical shrinking or vertical stretching is a nonrigid transformation. This means that the graph causes a distortion, or in other words, a change in the shape of the original graph. Shifting and reflections are called rigid transformations because the shape of the graph does not change. Vertical stretches and shrinks are called nonrigid because the shape of the graph is distorted. Stretching and shrinking change the distance a point is from the x-axis by a factor of c. For example, if g(x) = 2f(x), and f(5) = 3, then (5,3) is on the graph of f. Since g(5) = 2f(5) = 2*3 = 6, (5,6) is on the graph of g.
Graph of a bicycle
Reward as a function of passion
Mathematical PerspectiveThe point (5,3) is being stretched away from the x-axis by a factor of 2 to reach the point (5,6).
Let c be a positive real number. Then the following are vertical shifts of the graph of y = f(x) a) g(x) = cf(x) where c>1. Stretch the graph of f by multiplying its y coordinates by c If the graph of is transformed as: 1. , then the graph has a vertical stretch.
2. , then the graph has a vertical shrink.
3. , then the graph has a horizontal shrink.
4. , then the graph has a horizontal stretch.
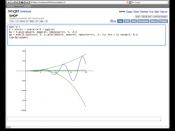
Graphs also have a possible horizontal shift. This is a rigid transformation because the basic shape of the graph is unchanged. In the example y = f(x), the modified function is y = f(x-a), which results in the function shifting a units. Some transformations can either be a horizontal or a vertical shift. For example, the following graph shows f(x) = 1.5x - 6 and g(x) = 1.5x - 3. The graph of g can be considered a horizontal shift of f by moving it two units to the left or a vertical shift of f by moving it three units up. Here is an example of this: Another example could be this. When looking at , the x-intercept of occurs when This would be a shift to the left one unit. When looking at , the x-intercept of occurs when This would be a shift to the right three units.
Lastly, another possible shift of graph is a vertical shift. This is a rigid transformation because the basic shape of the graph is unchanged. An example of a vertical shift : y = f(x) + a. The graph of this has exactly the same shape, but each of the values of the old graph y = f(x) is increased by a (or decreased if a is negative). This has the effect of picking up the entire function and moving up a distance a from the horizontal, or x axis. Let c be a positive real number. Then the following are vertical shifts of the graph of y = f(x): a) g(x) = f(x) + c Shift f upward c units b) g(x) = f(x) "" cShift f downward c units Let c be a positive real number. Vertical shifts in the graph of y + f(x): Vertical shifts c units upward: h(x) = f(x) + c. Vertical shift c units downward: h(x) + f(x) "" c.
The vertical shifts can by accomplished by adding or subtracting the value of c to the y coordinates.
Graphs have possible shifts of vertical shrinking and vertical stretching, horizontal shifts, and vertical shifts. These are the examples of the shifts that are possible for graphs.
More on the Taylor series
See the World Through My Eyes and Explore the Mote...
Graph of the function f(x)=x 3 - 9x