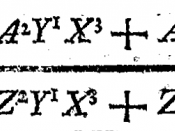There are two main ways to solve equations, algebraically or by using matrices. There are also different subcategories of each way to solve the equations. Using matrices or solving algebraically has some differences and similarities.
There are a few ways to solve equations algebraically. One line of attack is by substitution. In substitution, the goal is to solve for one of the variables in the first equation then substitute that variable into the second equation. Another approach is to solve by the linear combinations method. In linear combinations, the objective is to multiply one or both equations by a number so that adding the 2 equations can terminate one of the variables. Also, there is an additional way to solve equations, by graphing them and finding the point of intersection.
Matrices can solve equations, like solving equations algebraically. Cramer's rule is one method of solving equations through matrices. For Cramer's rule, to solve for a variable, replace a column in the coefficient matrix with the solution matrix.
Equation for z from Page 657 of Gabriel Cramer's b...
English: Screenshot of the SAGE mathematics softwa...
English: Markov chain, two possible states. The ch...Then find the determinant of the new matrix formed and divide it by the determinant of the coefficient matrix. When solving equations using the inverse, find the inverse of the coefficient matrix and multiply it by the solution matrix to get the values of x and y. A different process is to use augmented matrices. For this interchange two rows, multiply a row by a nonzero number, then add a multiple of one row to another row.
Algebraically solving equations and using matrices have their differences and their similarities. For example, they are different ways of achieving the same answer. Some people prefer using matrices in some areas, but in others they believe it would be easier solving the equations through algebra. For matrices, you are able to use all the methods...