Finding Zeroes of Functions Introduction: It is easy to graph lines and find their x-intercepts. You will be guided through the basic ideas of Newton's Method, which uses x-intercepts of appropriate lines to approximate x-intercepts of more difficult functions. Note: We need zeroes of a function y to find its x-intercepts; zeroes of y' to find stationary points of y; and zeroes of y'' to find possible points of inflection of y. Sometimes we just need to find where two functions cross. Many calculators use Newton's Method with y=x2-a and an initial guess of 1 to find the square root of a.
Elements of this lab were adapted from Solow's "Learning by Discovery", Edwards & Penney's "Single Variable Calculus", and Harvey & Kenelly's "Explorations with the TI-85". More information can be found in the annotated Bibliography at http://www.southwestern.edu/~shelton/Files/ in the list of Word files.
THEORY Let y = f(x) be a function.
calculus
Graph of sliding derivative line
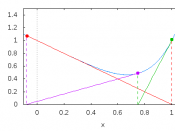
Animation of Newton methodOn the figure below, graph the tangent line to f(x) at x0. Label the point (x0, f(x0)), the graph y=f(x), the tangent line T1(x), the root r of y=f(x), and the x-intercept x1 of the tangent line.
Is the zero of the tangent line close to the zero of the function? Give a reason for your answer.
What is the equation of the line T1(x) tangent to the graph of f at (x0,f(x0))? Show that the x-intercept of T1(x), x1, is given by x1= x0-f(x0)/f'(x0) .
We repeat the process, using x1 as our new value at which to draw the tangent line. The x-intercept of the new line is x2. On the figure above, sketch the tangent lines T1 and T2. Show x1 , and x2. Show x3, if possible.
Write a formula for x2 in terms of x1.
Write a formula for xn+1 in terms of xn.
MATHEMATICA Define f[x_]:=x3 - 4 x2 - 1 .
Plot it with x in the interval [-10,10].
Use the mouse to estimate the x value of the root. Define x[0] to be 5 the first time.
Find the derivative of f[x] = x3 - 4 x2 - 1.
Here are the two steps for a single iteration: Calculate the next x: x[n+1]=x[n] - f[ x[n] ] / f'[ x[n] ] Increment n.
Perform several iterations.
Newton's Method does not always work well. It is sensitive to your initial guess.
Use Newton's Method on the same function with x[0] = 2. Notice that the Method does not converge to the root. What seems to be happening? Plot y4[x]=3 sinx and y5[x]=lnx with xmin=-5, xmax=30, ymin=-5, and ymax=5. Note that they intersect several times. To find these intersections, perform Newton's method with f[x_]:=y4[x]-y5[x].
Begin with x[0]=3.
Choose several other x[0].
English: Computergraphical study of the critical p...
English: Julia set for the rational function assoc...
English: Graph showing the failure of Newton's met...