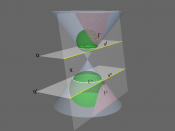
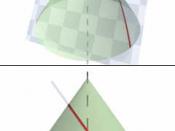
Conics are surprisingly easy! There are four types of conic sections, circles, parabolas, ellipses, and hyperbolas. The first type of conic, and easiest to spot and solve, is the circle. The standard form for the circle is (x-h)^2 + (y-k)^2 = r^2. The x-axis and y-axis radius are the same, which makes sense because it is a circle, and from
In order to graph an ellipse in standard form, the center is first plotted (the (h, k)). Then, the x-radius is plotted on both sides of the center, and the y-radius is plotted both up and down. Finally, you connect the dots in an oval shape. Finally, the foci can be calculated in an ellipse. The foci is found in the following formula, a^2 ÃÂ b^2 = c^2. A is the radius of the major axis and b is the radius of the minor axis. Once this is found, plot the points along the major axis starting from the center and counting c amount both directions.
In order to determine if an equation is an ellipse, the following three criteria must be met. There must be an x^2 and a y^2 just like in a circle. However, the coefficients of the x^2 and y^2 must be different. Finally, the signs must be the same. For example, equation 4 is an ellipse. 49x^2 + 25y^2 +294x ÃÂ 50y ÃÂ759 = 0 has an x^2 and a y^2. It also has different coefficients in front of them, and finally, both have the same sign! There you have it, an ellipse!HyperbolasBoy, now it is starting to get tough! But donÃÂt worry, hyperbolas are not much more difficult than ellipses. Imagine two parabolas opposite each other either going up and down or left and right. There is a distance separating the vertices of both parabolas, and that is what a hyperbola looks like. The standard form for the hyperbola is either ((x-h)/(rx))^2 ÃÂ ((y-k)/(ry))^2 = 1 or ((y-k)/(ry))^2 ÃÂ ((x-h)/(rx))^2 = 1. Notice the change between a hyperbola and an ellipse is that the signs are different! If the negative sign is in front of the y, then the hyperbola will be horizontal, and if the negative sign is in front of the x, then the hyperbola will be vertical. Once again, the (h, k) is the center. The slope of the asymptotes is simply plus or minus ry/rx. The transverse is also called the major axis in a hyperbola. However, it might not be the longest. The transverse is the positive radius in a hyperbola. The conjugate is therefore the negative radius.
In order to graph a hyperbola, take the center, and make four points marking the radius of the x and y like in an ellipse. However, this time, a box is drawn connecting the four dots, and a diagonal through the center to each corner of the box is drawn. This is called the asymptote. Finally, depending on which way the hyperbola is, the corresponding two opposite end radius points are used to draw a parabola like curve that reaches but does not touch the asymptote. The foci can be found in a hyperbola by using a^2 + b^2 = c^2. Where a and b are the lengths of the x-radius and y-radius, and c is equal to the distance from the center to the foci in both directions. Again remember, the foci must be on the transverse axis!In order to determine if an equation is a hyperbola, the following three criteria must be met. There must be an x^2 and a y^2 just like in a circle. However, the coefficients of the x^2 and y^2 must be different. Finally, the signs must be also different. For example, equation 3 is a hyperbola. 16x^2 ÃÂ 9y^2 ÃÂ 96x ÃÂ 36y ÃÂ468 = 0 has an x^2 and a y^2. It also has different coefficients in front of them, and finally, both have the different signs! Therefore, the equation is a hyperbola!ParabolasThe essential difference between parabolas and the three other conics is that parabolas do not have both an x^2 and a y^2. Instead, parabolas only have one, either the x or the y. Parabolas are essentially half of the hyperbola. The standard form of the parabola is y-k = a(x-h)^2, which is a vertical parabola, or x-h = a(y-k)^2. In this case, the (h, k) will be the vertex of the hyperbola. The a determines the direction of the opening of the parabola and the size of the parabola. If a is negative, then if the parabola is vertical, it opens down. If the parabola is horizontal, it opens to the left. If a is positive, then if the parabola is vertical, it opens up. If the parabola is horizontal, it opens down. If a is greater than or equal to the absolute value of 1, then the opening is narrow. The nearer to 0 a is, the wider the parabola becomes. Another form of the parabola is y=ax^2 + bx + c.
In order to graph a parabola, the vertex is first graphed. Next, you substitute in a value of x or y depending on which would make an integer or an easy number to graph. By substituting in an x, you can get the value of y and vice versa, and plot those points. Thus, the parabola is created. Finally, the axis of symmetry in a parabola is dependent upon whether the parabola is horizontal or vertical. If horizontal, then the axis of symmetry would be y = k in (h, k), and if vertical, then the axis of symmetry would be x = h.
In order to determine if an equation is a parabola, the following criteria must be met. There must be only one of either x^2 or y^2. For example, equation 2 is a parabola. 3y^2 ÃÂ 4x +12y ÃÂ 8 = 0 only has one, y^2 so it canÃÂt be a hyperbola, circle, or ellipse. It has to be a parabola!BibliographyWeisstein, Eric W. "Conic Section." From MathWorld--A Wolfram Web Resource. .