Question 1
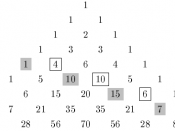
(a) The Fibonacci sequence can be achieved from Pascal's triangle by adding up the diagonal rows. Refer to Figure 1.1
Figure 1.1
This is possible as like the Fibonacci sequence, Pascal's triangle adds the two previous (numbers above) to get the next number, the formula if Fn = Fn-1 + Fn-2. Pascal's Triangle is achieved by adding the two numbers above it, so uses the same basic principle. This is why there is a relationship. The reason that it is added diagonally is because of how the numbers are added down and not across like in the Fibonacci sequence, but it is a lot like the Fibonacci sequence so it makes you think if the Fibonacci sequence was written out differently if it would have all these pattern in it, but its not part of the assignment to investigate that. It is possible to assume that it is possible for the Fibonacci sequence to have been created from Pascal's triangle as I don't know where the notion of the Fibonacci sequence was created for but it appears that other number patterns have been created from Pascal's triangle so why couldn't it be possible that it was.
Of course it works the opposite diagonal way as well.
(b) i. Powers of 2 has a relationship to Pascal's triangle, See Appendix 1 at end of assignment for picture. As you can see in the Appendix The sum of the row is equal to the powers of 2. for example
Power's of 2 Pascal's Triangle
2^0 1
2^1 2
2^2 4
2^3 8
2^4 16
Row 1 1
Row 2 2
Row 3 4
Row 4 8
Row 5 16
This is amazing as it is saying that the sum of each row in Pascal's triangle is a...