Leonardo Pisano(1170-1250) was an Italian number theorist, who was con-sidered to be one of the most talented mathematicians in the Middle Ages.
However, He was better known by his nickname Fibonacci, as many famoustheorems were named after it. In addition to that, Fibonacci himself some-times used the name Bigollo, which means good-for-nothing or a traveller. Thisis probably because his father held a diplomatic post, and Fibonacci travelledwidely with him. Although he was born in Italy, he was educated in NorthAfrica and he was taught mathematics in Bugia. While being a 'bigollo', hediscovered the enormous advantages of the mathematical systems used in thecountries he visited.
Fibonacci's contributions to mathematics are remarkable. Even in the worldtoday, we still make daily use of his discovery. His most outstanding contributionwould be the replacement of decimal number system. Yet, few people realizedit. Fibonacci had actually replaced the old Roman numeral system with theHindu-Arabic numbering system, which consists of Hindu-Arabic(0-9) symbols.
A simple plot of the numbers of the Fibonacci sequ...
English: Characterization of the Fibonacci word by...
Computation of the 7th number of the Fibonacci seq...There were some disadvantages with the Roman numeral system: Firstly, it didnot have 0's and lacked place value; Secondly, an abacus was usually requiredwhen using the system. However, Fibonacci saw the superiority of using Hindu-Arabic system and that is the reason why we have our numbering system today.
1He had included the explanation of our current numbering system in his book\Liber Abaci". The book was published in 1202 after his return to Italy. It wasbased on the arithmetic and algebra that Fibonacci had accumulated during histravels.
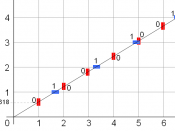
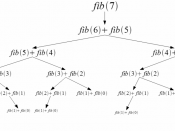
In the third section of his book \Liber Abaci", there is a math questionthat triggers another great invention of mankind. The problem goes like this:A certain man put a pair of rabbits in a place surrounded on all sides by awall. How many pairs of rabbits can be produced from that pair in a year if it issupposed that every month each pair begets a new pair, which from the secondmonth on becomes productive? This was the problem that led Fibonacci to theintroduction of the Fibonacci Numbers and the Fibonacci Sequence. What isso special about the sequence? Let's take a look at it. The sequence is listed asSn=f1, 1, 2, 3, 5, 8, 13, 21, 34, 55, g(1)Starting from 1, each number is the sum of the two preceding numbers. Writingmathematically, the sequence looks likeSn=f8 i > 2; i 2 Z; ai = aiôÂÂÂ2 + aiôÂÂÂ1 where a1 = a2 = 1g(2)The most important and inuential property of the sequence is that the higherup in the sequence, the closer two consecutive Fibonacci numbers divided byeach other will approach the golden ratio1, ' = 1+p52 1:61803399. The proveis easy. By de nition, we have' = a+ba = ab(3)From '=ab , we can obtain a = b'. Then, by plugging into Equation 3, we willget b'+bb' = b'b . Simplify, we can get a quadratic equation '2 ô ' ô 1 = 0.
Solving it, ' = 1+p52 1:61803399. The golden ratio was widely used in theRenaissance2 in painting. Today, Fibonacci sequence is still widely used inmany di erent sectors of mathematics and science. For example, the sequenceis an example of a recursive sequence, which de nes the curvature of naturallyoccurring spirals, such as snail shells and even the pattern of seeds inoweringplants. One interesting fact about Fibonacci Sequence is that it was actuallynamed by a French mathematician Edouard Lucas in the 1870's.
Other than the two well-known contributions named above, Fibonacci hadalso introduced the bar we use in fractions today. Previous to that, the numer-ator had quotation around it. Furthermore, the square root notation is also a1Two quantities a and b are said to be in the golden ratio if a+ba =ab='.
2The Renaissance was a cultural movement that spanned roughly the 14th to the 17thcentury, beginning in Florence in the Late Middle Ages and later spreading to the rest ofEurope. It was a cultural movement that profoundly a ected European intellectual life in theearly modern period.
2Fibonacci method, which was included in the fourth section of his book \LiberAbaci".
There are not only common daily applications of Fibonacci's contribu-tions, but also a lot of theoretical contributions to pure mathematics. Forinstance, once, Fibonacci was challenged by Johannes of Palermo to solve aequation, which was taken from Omar Khayyam's algebra book. The equationis 10x+2x2+x3 = 20. Fibonacci solved it by means of the intersection of a circleand a hyperbola. He proved that the root of the equation was neither an integernor a fraction, nor the square root of a fraction. Without explaining his meth-ods, he approximated the solution in sexagesimal3 notation as 1.22.7.42.33.4.40.
This is equivalent to 1 + 2260 + 7602 + 42603 + , and it converts to the decimal1.3688081075 which is correct to nine decimal places. The solution was a re-markable acheivement and it was embodied in the book \Flos".
\Liber Quadratorum" is Fibonacci's most impressive piece of work, althoughit is not the work for which he is most famous for. The term \Liber Quadra-torum" means the book of squares. The book is a number theory book, whichexamines methods to nd Pythogorean triples. He rst noted that square num-bers could be constructed as sums of odd numbers, essentially describing aninductive construction using the formula n2 + (2n + 1) = (n + 1)2. He wrote:I thought about the origin of all square numbers and discovered that theyarose from the regular ascent of odd numbers. For unity is a square and fromit is produced the rst square, namely 1; adding 3 to this makes the secondsquare, namely 4, whose root is 2; if to this sum is added a third odd number,namely 5, the third square will be produced, namely 9, whose root is 3; andso the sequence and series of square numbers always rise through the regularaddition of odd numbers. Thus when I wish to nd two square numbers whoseaddition produces a square number, I take any odd square number as one of thetwo square numbers and I nd the other square number by the addition of allthe odd numbers from unity up to but excluding the odd square number. Forexample, I take 9 as one of the two squares mentioned; the remaining squarewill be obtained by the addition of all the odd numbers below 9, namely 1, 3, 5,7, whose sum is 16, a square number, which when added to 9 gives 25, a squarenumber.
Fibonacci's contribution to mathematics has been largely overlooked. How-ever, his work in number theory was almost ignored and virtually unknownduring the Middle Ages. The same results appeared in the work of Maurolicothree hundred years later. Apart from pure math theories, all of us should bethankful for Fibonacci's work, because what we have been doing all the time,was his marvelous creation.
3Sexagesimal is of base 60.
3References[1] Deb Russell. A short Biography of Leonardo Pisano Fibonacci. RetrievedNovember 13, 2009, from About.com:http://math.about.com/od/mathematicians/a/ bonacci.htm[2] J. J. O'Connor E. F. Robertson. Leonardo Pisano Fibonacci. RetrievedNovember 13, 2009, from GAP-Groups, Algorithms, Programming-aSystem for Computational Discrete Algebra:http://www.gap-system.org/ history/Biographies/Fibonacci.html[3] Wikipedia contributors. Goldenratio. Retrieved November 13, 2009, from Wikipedia, The Free Encyclopedia:http://en.wikipedia.org/w/index.php?title=Golden ratio&oldid=322450397[4] Wikipedia contributors. Renaissance. Retrieved November 13, 2009, fromWikipedia, The Free Encyclopedia:http://en.wikipedia.org/w/index.php?title=Renaissance&oldid=3217603544
English: A terribly flawed plot that's supposed to...
Fibonacci Fractal
English: The 24 repeated numbers of the digital ro...