Indian Real estate

8/5/2014

1

Session XII

Problem solving: sampling distributions

Interval estimation of

population mean, proportion and variance

Exercise with sampling

distributions

1 2 16 , , observations drawn from a NORMAL population

with both mean and variance 100. Find

i) P(Sum > 1550)

ii) P( sample mean < 100 - 0.5 * sample SD)

iii) P( sample SD > 12)

X X X…

3

Practice Problem

Gotchya runs an entertainment centre. The following data is

from 27 random selected weeknights about number of paying

patrons. His accountants tell him that they need to have at least

fifty five patrons in order to break even on a weeknight.

The partners want to operate on weeknights if they can be at

least 95 percent certain that they will break even at least half

the time. Should Gotchya continue to stay open on weeknights?

The no. of paying patrons on 27 randomly selected weeknights:

61 57 53 60 64 57 54 58 63

59 50 60 60 57 58 62 63 60

61 54 50 54 61 51 53 62 57 4

Solution to Practice problem

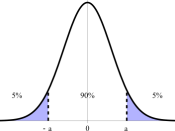
Does the 95% C.I. for π stay above 0.5? Where

π= proportion of breakeven weeknights (# of customers 55 or more)

n=27 sample proportion p = 19/27=0.7037

(1 ) .7037 .2963ˆ. .( ) . .( ) 0.0878 27 27

S E p S E p π π− ×

= ⇒ = =

So, the 1-sided 95% C.I. for π is = (0.7037 - 1.645 × 0.0878 = 0.5591, 1)

Since the 95% CI is above 0.50, the owner can be more 95% certain

that they would break even at least half the time and decide to stay

open on weeknights too.

Sample Size Determination

in

Estimating Mean and proportion

6

Determine n in estimating µ

to a given...