hat P(N): N-> N is countable b) This means that Pi(N) is enumerable P0, P1, P2, such that Pi(N) = a subset of N c) Now consider a function g where g(n) = Pi(n) + 1 d) g must be some subset Pi(n) for some i. But this is impossible considering that Pi(i) = g(i) = Pi(n) + 1 e) After canceling, 0 = 1 which is impossible.
f) Therefore P(N): N -> N is uncountable.
2) Show that there are only countably many texts, where text is a finitely long string of symbols, whose symbols are chosen from a finite alphabet.
Reference: Jason Seemann a) Given a finite length, each position of the length can be mapped to some x existing in N.
b) Given a finite alphabet, each symbol in the alphabet can be mapped to some y existing in N.
c) Given these 2 suppositions, any finite series of symbols can be represented by concatenating the symbol's x position and the symbol's y value.
Фридрих Вильгельм Бессель,...
Weight Matrix
Halting problem 3d) e.g.
Consider: Symbols: a, b, c Mapping a->1, b->2, c->3 Now consider the text "abc". This is mapped to 112233.
Consider: Symbols: a, a, a Mapping a->1, a->1, a->1 Now consider the text "aaa". This is mapped to 111111.
e) Because each symbol and position is represented by a 1-1 relationship with N, we can guarantee that each possible text will be unique.
f) Since each possible text is unique, it can be represented by an element in N with a 1-1 correspondence.
g) As shown above, we have created a function that for every given text, it has a 1-1 mapping with the set N. f: N-> S | (f(i) = s(i)) 3) Show that the following problem is undecidable using the undecidability of the Halting problem.
For any function F: A->B determine whether or not F is total.
In other words, prove that the function: Total(F) = 1 if F is total 0 otherwise is computed by no effective procedure.
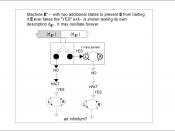
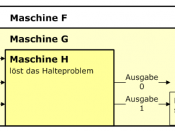
Given: Halting problem is undecidable.
a) For the sake of contradiction, suppose that total(F) exists.
1) Read p. (p | p is a program and |p| <= n) 2) Read n. (n is number of inputs) 3) Set answer := 0; 4) for i = 0 to p do: for j = 0 to n do: if (halt (p,n) = 0) then (*0 means not halt, 1 means halt*) Reassign answer:= 1 5) Write answer.
b) Step 4 is effective by assumption. If a program q does not halt, it is considered total.
c) By Church-Turing thesis one can turn this procedure into a program of our language(in this case, Pascal).
d) The conclusion is that the Halting program is computable by a program in this language is a contradiction with our previous proposition.
e) Therefore, the unjustified assumption that a procedure to compute the function Total exists must be false.
4) Consider the addition program written in the WHILE found in chapter 2 of the book page 35.
a) Show a derivation of this program in grammar.
b) Explain its evaluation step by step when computing the while equivalent of "3+2", showing the intermediate stores.
a) Derivation: read XY; X:= hd XY; Y:= tl XY; WHILE X DO {Y:=cons nil Y; X:= tl X;}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {Y:=cons nil Y; X:= tl E;}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {Y:=cons nil Y; X:= E;}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {Y:=cons nil Y; D}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {Y:=cons E Y; D}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {Y:=cons E F; D}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {Y:=E; D}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {C; D}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE X DO {C}; WRITE Y read XY; X:= hd XY; Y:= tl XY; WHILE E DO {C}; WRITE Y read XY; X:= hd XY; Y:= tl XY; D; WRITE Y read XY; X:= hd XY; Y:= tl E; D; WRITE Y read XY; X:= hd XY; Y:= E; D; WRITE Y read XY; X:= hd XY; C; D; WRITE Y read XY; X:= hd XY; C; WRITE Y read XY; X:= hd E; C; WRITE Y read XY; X:= E; C; WRITE Y read XY; D; C; WRITE Y read XY; C; WRITE Y b) Stores: [Values in brackets indicate the Numeral evaluation of nil statements] XYXYCode Fragment ((nil.(nil.(nil.nil))).(nil.(nil.nil)))read XY; (nil.(nil.(nil.nil)))[3]X:=hd XY; (nil.(nil.nil))[2]Y:=tl XY; (nil.(nil.(nil.nil)))[3]WHILE X DO (nil.(nil.(nil.nil)))[3]Y = succ Y; (nil.(nil.nil))[2]X = pred X; (nil.(nil.nil))[2]WHILE X DO (nil.(nil.(nil.(nil.nil))))[4]Y = succ Y; (nil.nil)[1]X = pred X; (nil.nil)[1]WHILE X DO (nil.(nil.(nil.(nil.(nil.nil)))))[5]Y = succ Y; nil [0]X = pred X; nil [0]WHILE X DO (nil.(nil.(nil.(nil.(nil.nil))))) [5]WRITE Y Y gets outputted as answer. X is 0. The final result of Y is 5 which is the correct assessment of "3+2".
5) Write a 'multiplication' program in WHILE (you may call addition from inside this one).
read XY; (* Multiply X Y* ) X := hd XY; (*Read in the first number* ) Y := tl XY; (*Read in the second number* ) answer := nil; counter := Y(*Sets a counter to Y,*) (* this way, Output add X Y times which is same as XxY*) while counter do (*also, Value X and Y are left untouched answer := addition (cons answer X); (*Calls the addition functions*) counter := pred counter; (*Decrements counter*) write answer(*Outputs answer*) Document converted from ms word 8 by MSWordView(mswordview 0.5.14 (bw6)) MSWordView written by Caolan McNamara
Halting problem 1
English: Graphical proof sketch: the Halting probl...
Vrin-Cons