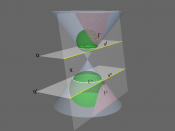
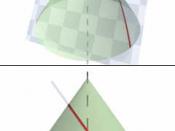
Conic sections is by definition the intersection of a plane and a cone. By changing the angle and location of the intersection, we can produce a circle, ellipse, parabola or hyperbola; or in the special case when the plane touches the vertex: a point, line or 2 intersecting lines. The general equation for the conic sections is: Ax2 + Bxy + Cy2 + Dx + Ey + F = 0.
Parabolas are used in real life situations such as the building of suspension bridges, the reflector of automobile headlights, and in physics with laws of gravity and the path for thrown objects such as javelins. Satellite dishes and radio telescopes are also built in the shape of parabolas. Important terms of parabolas include vertex, zeros, and y intercept.
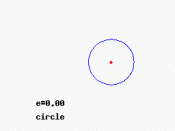
Circles are seen and used almost everywhere, from the wheels on our cars to electric saws. Even rainbows come in arcs of a circle.
English: animated gif of conic sections, morphing ...
Conic Section (Hyperbola)
English: Parabola as a conic section Dansk: Viser ...Some important terms include: radius, origin (or center), and diameter.
Ellipses were first claimed by Kepler to be the true shape of the orbital. Today, ellipses are also used in the manufacturing of optical glass for telescopes and microscopes.
Some key terms of ellipses are foci and origin.
Some key terms of hyperbola terms are: branch, center, Conjugate Axis, asymptotes, and transverse axis.
Hyperbolas are used to illustrate the path of a comet. Sound waves also travel in hyperbolic paths.
Rainbows
i'm not much of a math wiz, but i do know that rainbows come in full circles, not arcs. sometimes the arc is all you can see of the rainbow though.
1 out of 1 people found this comment useful.