Introduction
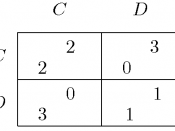
Prisoner's dilemma
Will the two prisoners cooperate to minimize total loss of liberty or will one of them, trusting the other to cooperate, betray him so as to go free?
Many points in this article may be difficult to understand without a background in the elementary concepts of game theory.
In game theory, the prisoner's dilemma is a type of non-zero-sum game in which two players try to get rewards from a banker by cooperating with or betraying the other player. In this game, as in many others, it is assumed that the primary concern of each individual player ("prisoner") is self-regarding; i.e., trying to maximise his own advantage, with less concern for the well-being of the other players.
In the prisoner's dilemma, cooperating is strictly dominated by defecting (i.e., betraying one's partner), so that the only possible equilibrium for the game is for all players to defect. In simpler terms, no matter what the other player does, one player will always gain a greater payoff by playing defect.
Since in any situation playing defect is more beneficial than cooperating, all rational players will play defect.
The unique equilibrium for this game does not lead to a Pareto-optimal solution--that is, two "rational" players will both play defect even though the total reward (the sum of the reward received by the two players) would be greater if they both played cooperate. In equilibrium, each prisoner chooses to defect even though both would be better off by cooperating, hence the dilemma. One resolution of the dilemma proposed by Douglas Hofstadter in his Metamagical Themas is to reject the definition of "rational" that led to the "rational" decision to defect. Truly rational (or "superrational") players take into account that the other person is superrational, like them, and thus they cooperate. Many authors...