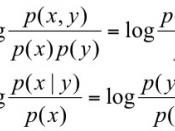Chapter 4 Outline
Determine sample spaces and find the probability of an event using classical probability or empirical probability.
Find the probability of compound events using the addition rules.
Find the probability of compound events using the multiplication rules.
Find the conditional probability of an event.
Determine the number of outcomes of a sequence of events using a tree diagram.
Find the total number of outcomes in a sequence of events using the fundamental counting rule.
Find the number of ways r objects can be selected from n objects using the permutation rule.
Find the number of ways r objects can be selected from n objects without regard to order using the combination rule.
Find the probability of an event using the counting rules.
Probability as a general concept can be defined as the chance of an event occurring. In addition to being used in games of chance, probability is used in the fields of insurance, investments, and weather forecasting, and in various areas.
Rules such as the fundamental counting rule, combination rule and permutation rules allow us to count the number of ways in which events can occur.
Counting rules and probability rules can be used together to solve a wide variety of problems.
Basic Concepts
A probability experiment is a chance process that leads to well-defined results called outcomes.
An outcome is the result of a single trial of a probability experiment.
A sample space is the set of all possible outcomes of a probability experiment.
An event consists of a set of outcomes of a probability experiment.
Basic Concepts (cont'd.)
Equally likely events are events that have the same probability of occurring.
Venn diagrams are used to represent probabilities pictorially.
Classical Probability
Classical probability uses sample spaces to determine the numerical probability that an event will happen.